Sampled Data Digital Control Systems

Warning

NOT LTI

The problem that we have here, are Continuous Time inputs that needs to be discretized for the controller, and then Discrete Time that needs to become analog for our continuous time output.

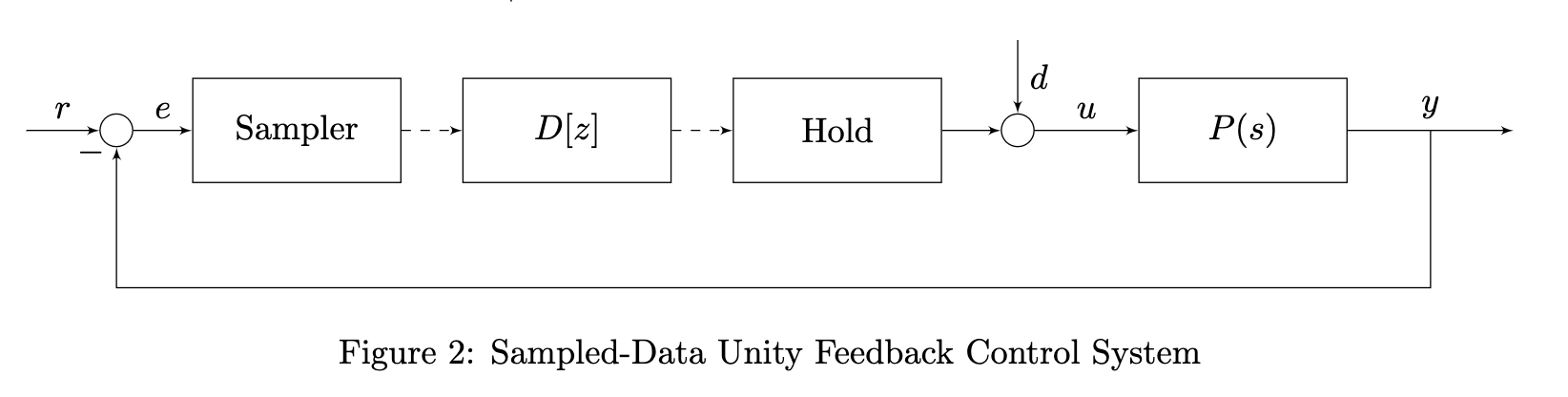
• D(s): CT plant
• D[z}]: DT controller
• r, d, u, y: all in CT
• A/D (sampler): samples at discrete intervals where T is the sampling time of the system
• D/A (zero order hold): holds u[k] for $t\in [kT,(k+1)T]\forall k\in \mathbb{Z}$

This system is not LTI. But we want to work with Linear Time Invariant systems because they are easier to work with. So our approach will be:

1. Attempt to choose T (or modify control architecture or control design) so the sampled-data system is approximately LTI.
2. Use LTI tools to perform control design
   1. Approximating CT controllers with DT controllers (Emulation Control Design)
   2. Direct Design of DT Controllers
3. Analyze and simulate the results on the true system

Note

The Closed Loop transfer functions are not well defined for SD systems.

Definition

The map (or function) from $\left[\begin{array}{c}r\\ d\end{array}\right]$ to $\left[\begin{array}{c}u\\ e\\ y\end{array}\right]$ is the function that sends r(t), d(t) to the resulting u(t), e(t), y(t).

This basically says that transfer functions can’t give us output signals from input signals but rather a function that accepts the internal signals can provide the output signals.

The main difference here, is that we need to consider the impact of both $r$ and $d$ at the same time

Related Concepts

• DAC
• ADC
• Sampling Time
• Closed Loop Stability for SD Systems
• Performance of SD Systems