Nonlinear State Space Models

Summary

Motivation: Sampled Data Digital Control Systems are not Linear Time Invariant, so we need to move beyond LTI models to be able to analyze sampled data systems.

Finding the actual state space models is the exact same for linear state space realizations.

See Drawing 2025-10-24 11.54.34.excalidraw for examples for this concept.

Rendered Excalidraw

For an LTI model $f(x,u)=Ax+Bu$ and $g(x,u)=Cx+Du$…

Definition

A non-linear state space model of a system is a model of the form…

• $x^{\prime }=f(x,u)$ (*)
• $y=g(x,u)$

such that for any initial condition $x(t=0)=x_0$ and any input signal $u(t)$, there exists a unique solution to Eq (*), and it is equal to the system’s output.

Note that this is time-invariant since neither functions depend on t

This is a general framework for modelling the dynamics of a system which gives us a well defined solution.

For regular linear State Space Models, we have 2 options as we approach infinity. We either approach 0 or infinity. In non-linear systems, there are other states that we can approach rather than just this binary choice.

Definition (Equilibrium Point)

What does steady state look like in non-linear systems?

Given a constant control signal $u(t)=\bar{u}\forall t\ge 0$ for some $\bar{u}\in \mathbb{R}$, an equilibrium point of a state space model is any state $x_e$ that satisfies $f(x_e,\bar{u})=0$.

Note

You find an equilibrium point, and then you can linearize about that point later!

$x^{\prime }=f(x_e,\bar{u})=0$ which implies that $x(t)=x_e\text{, x(t) is a constant}\forall t\ge 0$. Just set the state space realization to 0 and rearrange for the equilibrium points.

For an LTI system…
$x=f(x_e,\bar{u})=A{x}_e+\bar{B}u=0⟹x_e=-A^{-1}B\bar{u}$
If $\bar{u}=0⟹x_e=0$
LTI systems only have 1 equilibrium point for a fixed $u(t)$

Example

We can apply Linearization about $x^e,\bar{u}$. as follows…
We want linearization of the form…

• $f(x,u)=f(x^e,\bar{u})+\frac{\partial f}{\partial x}{|}_{x^e,u}(x-x^e)+\frac{\partial f}{\partial u}{|}_{x^e,u}(u-\bar{u})$
• $g(x,u)=g(x^e,\bar{u})+\frac{\partial g}{\partial x}{|}_{x^e,u}(x-x^e)+\frac{\partial g}{\partial u}{|}_{x^e,u}(u-\bar{u})$

Where $f$ is vector valued…

• $f(x,u)=\left[\begin{array}{c}{f}_1(x,u)\\ \dots \\ f_n(x,u)\end{array}\right]$
• $x=\left[\begin{array}{c}\frac{\partial f_1}{\partial u}\\ \dots \\ \frac{\partial f_n}{\partial u}\end{array}\right]$
• $\frac{\partial f_1}{\partial x_1}:=\left[\begin{array}{ccccc}\frac{\partial f_1}{\partial x_1}& & \dots & & \frac{\partial f}{\partial x_n}\\ \dots & & \dots & & \dots \\ \frac{\partial f_n}{\partial x_1}& & \dots & & \frac{\partial f_n}{\partial x_n}\end{array}\right]$
• $\frac{\partial f}{\partial u}:=\left[\begin{array}{c}\frac{\partial f_1}{u}\\ \dots \\ \frac{\partial f_n}{u}\end{array}\right]$
• $\frac{\partial g}{x}:=[\frac{\partial g}{\partial x}\dots \frac{\partial g}{\partial u}]$
• $\frac{\partial g}{\partial u}=\frac{\partial g}{\partial u}$

Summary

Basically our steps here are…

1. Find the equilibrium points $x^e$
2. Find the partial derivates of $f(x,u)$
3. Make the $\frac{\partial f}{\partial u}$ matrix and evaluate at ($x^e,\bar{u}$) (just sub in the values for these)
4. Put into the general linearized form

Definition

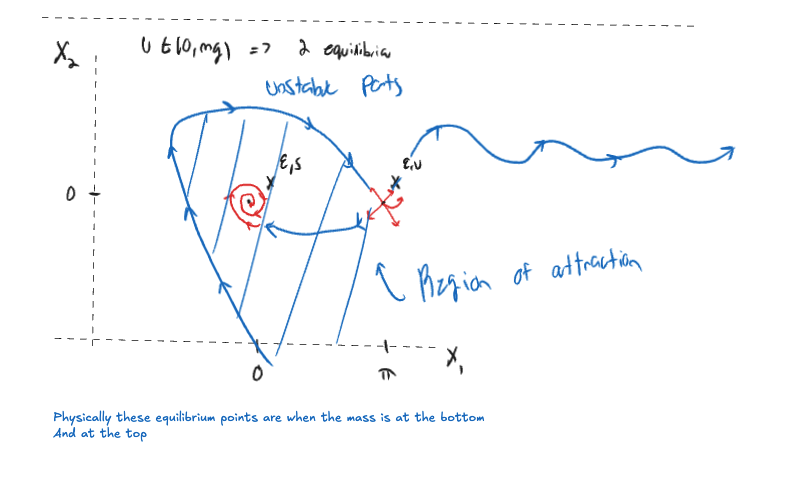
An equilibrium point $x^e$ is stable if all of the eigenvalues (Eigenvalues and Eigenvectors) of the linearization at $x^e\left(A=\frac{\partial f}{\partial x}\right){|}_{x^e,\bar{u}}$ are stable in $C^{-}1$

An equilibrium point which is not stable is called unstable.

Note

Note that $x^{e,u}$ is an unstable equilibrium point because it has an unstable eigenvalue ${\lambda }^u$.

Consider the linearization about $x^{e,s}=\left[\begin{array}{c}0\\ 0\end{array}\right]$.

$\Delta \dot{x}=\left[\begin{array}{ccc}0& & 1\\ -\frac{g}{l}& & -\frac{0}{ml}\end{array}\right]\Delta x+\left[\begin{array}{c}0\\ \frac{1}{ml}\\ B\end{array}\right]\Delta u$

$\Delta y=[10]\Delta x$

Assume $\Delta u=0$ $\forall t{\ge }_0$
$\Delta \dot{x}=A\Delta x$ and it can be shown that A has 2 stable eigenvalues

${\lambda }^s=\mathrm{Re}({\lambda }^s)+j\mathrm{Im}({\lambda }^s)$
$v^s$ eigenvector
$e^e,s$ is a stable equilibrium point

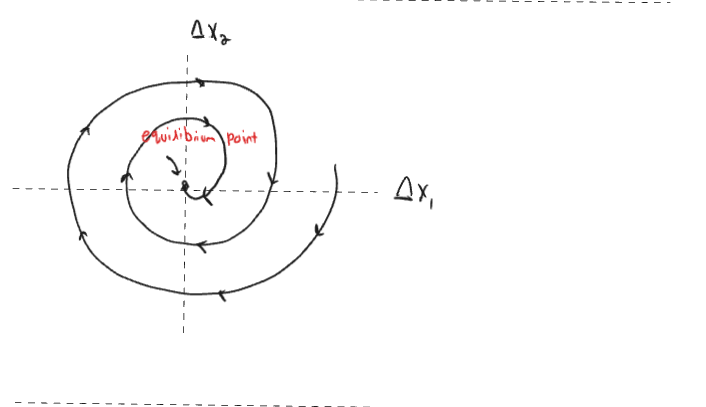
Linear systems are a pretty good approximation of non-linear systems around an equilibrium point.

Definition

The region of attraction of $x^{e,s}$ is the set of initial conditions $x^0$ such that $x(t=0)=x^0$ then ${\lim }_{t\to \infty }x(t)=x^{e,s}$. Where your stable equilibrium point is your desired operating point