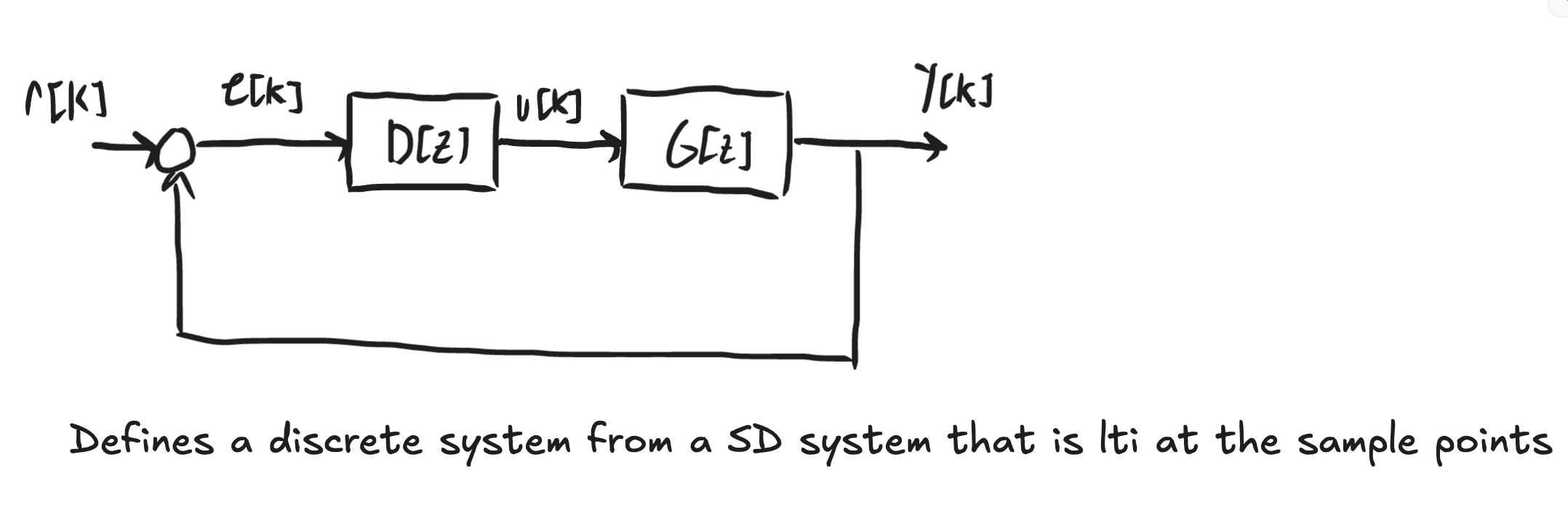
Closed Loop Stability for SD Systems

Closed loop stability for SD systems

The SD system is closed-loop stable if the map from $\left[\begin{array}{c}r\\ d\end{array}\right]$ to $\left[\begin{array}{c}u\\ e\\ y\end{array}\right]$ is BIBO stable.

Definition

The map from $\left[\begin{array}{c}{x}_1\\ \dots \\ x_n\end{array}\right]$ to $\left[\begin{array}{c}{y}_1\\ \dots \\ y_m\end{array}\right]$ is BIBO stable if for every collection of bounded signals $x_1(t)\dots x_n(t)$, the resulting signals are bounded $y_1(t)\dots y_m(t)$.

Definition (Pathological)

For a plant $P(s)$, a sampling time $T>0$ is pathological, if the number of poles of $G[z]$ is < the number of poles of $P(s)$

Note for almost all of $T>0$, T is almost guaranteed to be non-pathological

What is the consequence of being pathological?

• Theorem: For the SD system, if T is non-pathological, then the SD system is closed-loop stable iff its associated discrete time system is closed-loop stable.

How do we discretize a continuous jawn

See Direct Design of DT Controllers but for something with no integrator(s)…
$G[z]={\sum }_{i=1}^n\frac{c_i}{{\lambda }_i}\frac{e^{{\lambda }_{i}T}-1}{z-e^{{\lambda }_{i}T}}$

Whats the point of this?

• Now we have a link between sampled-data systems and discrete control systems
• We can use our old Stability methods to test the different types of stability
• What if we have a system that is a super high order which would make it hard to determine stability?
  • Shur Control Systems