Shur Control Systems

Definition

$\Delta [z]$ is Schur if roots($\Delta \subset \mathbb{D}$)

Lemma

Let $\Delta [z]={\sum }_{i=0}^n{c}_i{z}^i$

If $\Delta$ is Schur, then $|c_n|>|c_0|$

Basically saying the leading coefficient of the highest degree needs to be bigger in size than the ending coefficient of the smallest degree term.

There are however limitations to this lemma. If the lemma does not hold, then we know for sure that $\Delta$ is not Shur, but just because the lemma holds, $\Delta$ could still not be Shur.

Are We Shur?

Let $\Delta [z]={\sum }_{i=0}^n{c}_i{z}^i$ and $Q[z]={\sum }_{i=0}^n{c}_{n-i}{z}^i$ where this basically just flips the order of the coefficients where $\Delta$ is nth order.

We want a lower order polynomial for testing if $\Delta$ is Schur (instead of testing $\Delta$ directly). We could do this recursively or iteratively until we get to a low enough order that its really easy.

The idea here, is that we want to cancel out $c_0$ and divide by $z$, to give us a lower order polynomial.

To do this…
$\Delta [z]-\frac{c_0}{c_n}Q[z]={\sum }_{i=0}^n(c_i-\frac{c_0}{c_n}{c}_{n-i})z^i$

Where at $i=0⟹c_0-\frac{c_0}{c_n}{c}_n$ where the $c_n$ will cancel out eventually leading to $z{\sum }_{i=0}^{n-1}(c_{i+1}-\frac{c_0}{c_n}{c}_{n-i-1})z^i$ where this is $⟹zR[z]$

---

Final Equation $R[z]=\frac{1}{z}(\Delta [z]-\frac{c_0}{c_n}Q[z])$ and $R[z]$ is of order n-1.

---

Lemma

Suppose $|c_n|>|c_0|$
Then $\Delta [z]$ is Schur iff $R[z]$ is Schur

Lemma

Boundary crossing lemma…
Let $\lambda \in [0,1]$ and ${\Delta }_{\lambda }[z]={\Delta }^1[z]-\lambda {\Delta }^2[z]$ and if ${\Delta }^1[z]$ is Shur and ${\Delta }^1[z]-{\Delta }^2[z]$ is not Shur (or the other waya round), then there exists ${\lambda }^{\ast }\in [0,1]$ such that ${\Delta }_{{\lambda }^{\ast }}[z]$ has a root on the unit circle

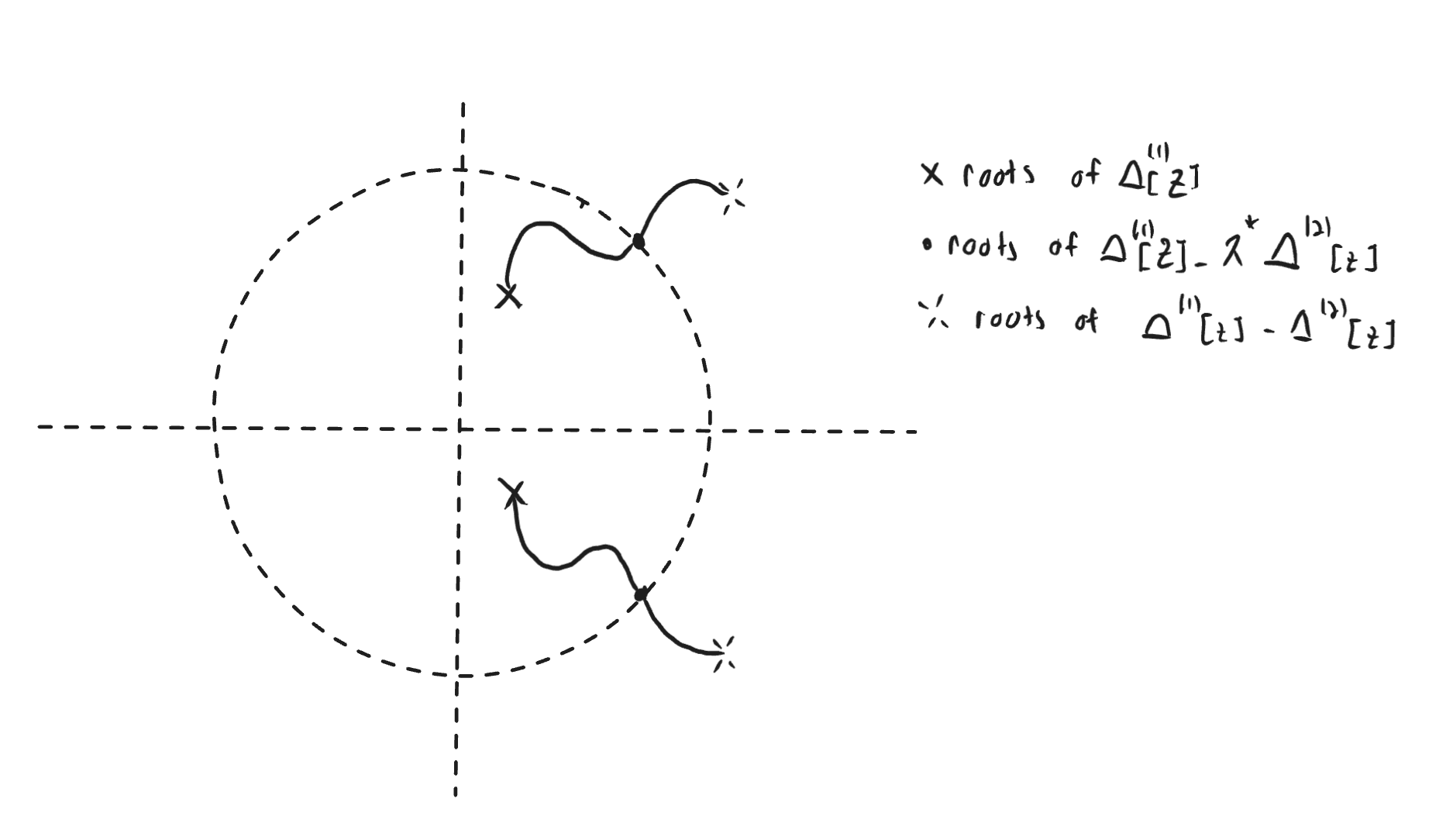
Proof by picture

Defining $R^0[z]=\Delta [z]$ we want to keep applying polynomial reduction such that we get an $R[z]$ of order 1 ($R^{n-1}[z]$)
At each stage we can check if our $R[z]$ at that given degree (stage) is Shur.
At any point if $R[z]$ is not Shur, we can stop.
We may need to go all the way until order 1 where $c_{1}z+c_0⟹$ has one root at $z=\frac{-c_0}{c_1}$ and $|z|=\frac{|c_0|}{|c_n|}<1$ which is our base case.

General Algorithm

• Given: $R^i[z]$ for some $i\in 0,\dots ,n$
• Check:
  • is $|c_n|>|c_0|$?
  • if not, $R^i[z]$ is not Shur [by the lemma from class, we can stop]
    • $R^{i-1}[z]$ is not Shur and $R^0[z]=\Delta [z]$ is not Shur [lemma from class]
  • if true, set $R^{i+1}[z]=\frac{1}{z}(R^i[z]-\frac{c_0}{c_n}{Q}^i[z])$ and repeat
• Stop with $R^{n-1}[z]$
  • Do coefficient Shur test and make decision

For each $R^i[z]$ we need to check if $|c_n|>|c_0|$. Assume $c_n>0$ (if not just multiply $\Delta$ by $-1$). Note that $|c_n|>|c_0|⟹$ $c_n-\frac{c_0}{c_n}{c}_0>0$ where $[c_n>0]$.

What is the point of this weird derivation?

• Jury Table