LL(1)

L: Left-to-right

• Parses the input from left to right L: Leftmost derivation
• Does a left-most derivation, we care about all our derivation strategies yielding the same results 1: 1 token lookahead
• Lexer.inspect()

The main idea

This is what we can easily parse by hand.
The main idea behind LL(1) parsers, is that we can determine which alternative to choose based on one token of lookahead. This is how we test if a grammar is LL(1).

Issues

LL(1) has a couple of issues that would prevent parsing…

• Left recursion
  • Left recursion looks like: $R\to Rbc$
  • In LL(1), we only look one ahead, which means this term expands indefinitely
  • Shift recursive term to the end and introduce a base case $ϵ$
  • 
• Prefix ambiguity
  • Prefix ambiguity looks like: $R\to bcc$, $R\to bab$
  • Here, you can see that the first token is the same, which is ambiguous for an LL(1) parser
  • We solve this with left-factoring
  • 

What we do here, is refactor the grammar to write a weakly equivalent grammar in EBNF using repetition that does not constrain the associativity.

LL(1) Analysis

Like I said earlier, a grammar is LL(1) or can be proved to be LL(1), if we can predict what alternative to choose based on a one token lookahead. In other words, can we derive predict sets that are disjoint, or unambiguous.

To do so, we need to derive these predict sets which can be done by following these steps:

• Convert grammar from EBNF to BNF
• Determine first sets for each non-terminal
• Determine predict sets for each production
  • This includes EPS and Follow sets as well

Convert Grammar from EBNF to BNF

EBNF:

• Includes * and | BNF:
• No stars and bars (add EOF $$ if requires)
• These are our productions Bars are easy to convert but for Kleene Stars…
• We need to introduce new non-terminals that do the repetition through recursion, where we need an epsilon to terminate the recursion.

This isn’t so hard:

A = B*
---
A = Tail
Tail = B Tail | eps

EPS

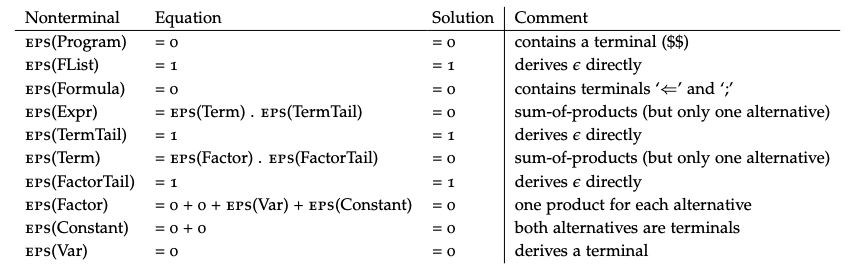
We need to determine which non-terminals can derive $ϵ$. If a non-terminal can do so, then its EPS function $EPS(X)=1$, otherwise 0. We can AND and OR, EPS’s together to get the final EPS result for a non-terminal.

• We use a + for alternatives and a $\cdot$ is used for terms together
• For a term like Factor, the contributions of Expr and Factor are - since the RHS contains terminals which evaluate to 0
• If a production has a terminal, it cannot be nullable (0)

First Sets

What is the first terminal for a non-terminal? Given a production, this is pretty easy to find by just following the non-terminal production to the first found terminal.

• There are additional rules though informed by the EPS
• Scanning from left to right from A = X_1X_2...X_n
  • If X_1 is a terminal, add that terminal to the first set and stop
  • If X_{1} is a non-terminal add FIRST{X_{1}} to the FIRST set of A, stop if X_{1} is non-nullable (EPS is 0), otherwise if X_{1} is nullable, stop going down X_{1} and move onto X_{2} repeating the same logic.

Follow Sets

The intuition of $Follow(A)$ is, what token might appear after A? We need EPS and First sets to compute these.

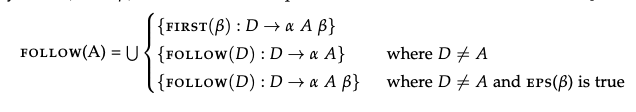
Basically look at all the productions to see if any of them match one of these three patterns, if they do, add them (union) to the follow set.

• What this means is look to the right of A, if there is a non-terminal, find the FIRST of that non-terminal since that can directly follow A.
• If the FIRST is a terminal, put the terminal in the set. If its a non-terminal, add the follow of that original non-terminal to the set (which means we need to follow it which will eventually lead to a terminal or $ϵ$).
• Pseudo:
  • If a non-terminal follows the non-terminal you care currently following. Then add the FIRST of that non-terminal to the set. If the non-terminal is nullable, also add the FOLLOW of that non terminal (through a union)

Program -> FList $$
FList -> Formula FList
FList -> eps
Formula -> Var '<=' Expr ';'
Var -> id

FOLLOW(Formula) = FOLLOW(FList) U FIRST(FList) => {$$ (from Program), id(the first non-terminal from var)}

Predict Sets

Now we can just use the equation below to compute the predict set…
Formalization
What does this mean?

• $\alpha$ is any grammar stuff, might just be a non-terminal N
• ⇒* signifies, “eventually” derives
• Basically, we want to eventually $ϵ$ (““) (Also called nullable), a terminal is never $ϵ$
• The key thing here, is that we need EPS and Follow if the grammar has an epsilon anywhere in it How do you actually do it?
• For every alternation for a production the predict set is the FIRST(RHS) $\bigcup$ FOLLOW of LHS if the RHS is nullable (EPS(RHS) == 0)
• We do this for every production

Disjoint

Two sets are called disjoint if they have no elements in common.

• If all of our predict sets for all productions are disjoint, then our grammar is LL(10)