Deterministic Finite Automaton

AKA DFA’s

Takes a finite input tape (string) input → Finite Automaton → Outputs “accept” or “reject” state

Machine Power

The computational power of a machine is quantified by the set of problems that machine can compute. If one machine can solve more problems than another, it is more powerful.

Transition Graph

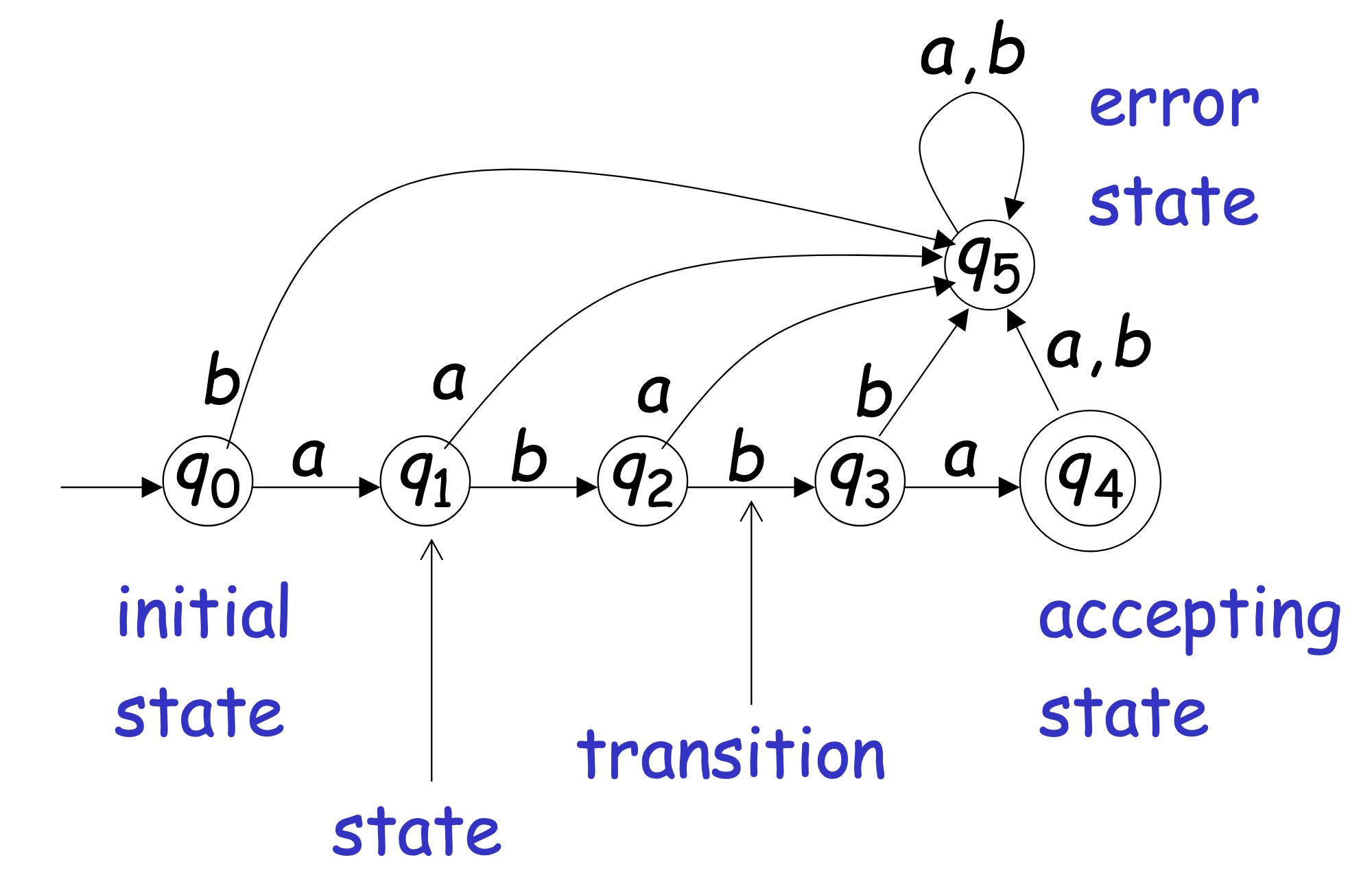
Here, the alphabet is $\Sigma =\left\{a,b\right\}$. To reach the accepting state, use the string “abba“

You can modify this automaton to accept different tapes but changing some q’s to be an accepting state. Ex. to accept the empty string, you just need to make $q_0$ and accepting state.

$M=\left(Q,\Sigma ,\partial ,q_0,F\right)$

• $Q$ = set of states
• $\text{Upsigma}$ = input alphabet
• $\partial$ = transition function
• $q_0$ = initial state
• $F$ = set of accepting states

You can also define a transition table for $\partial$ that looks like…

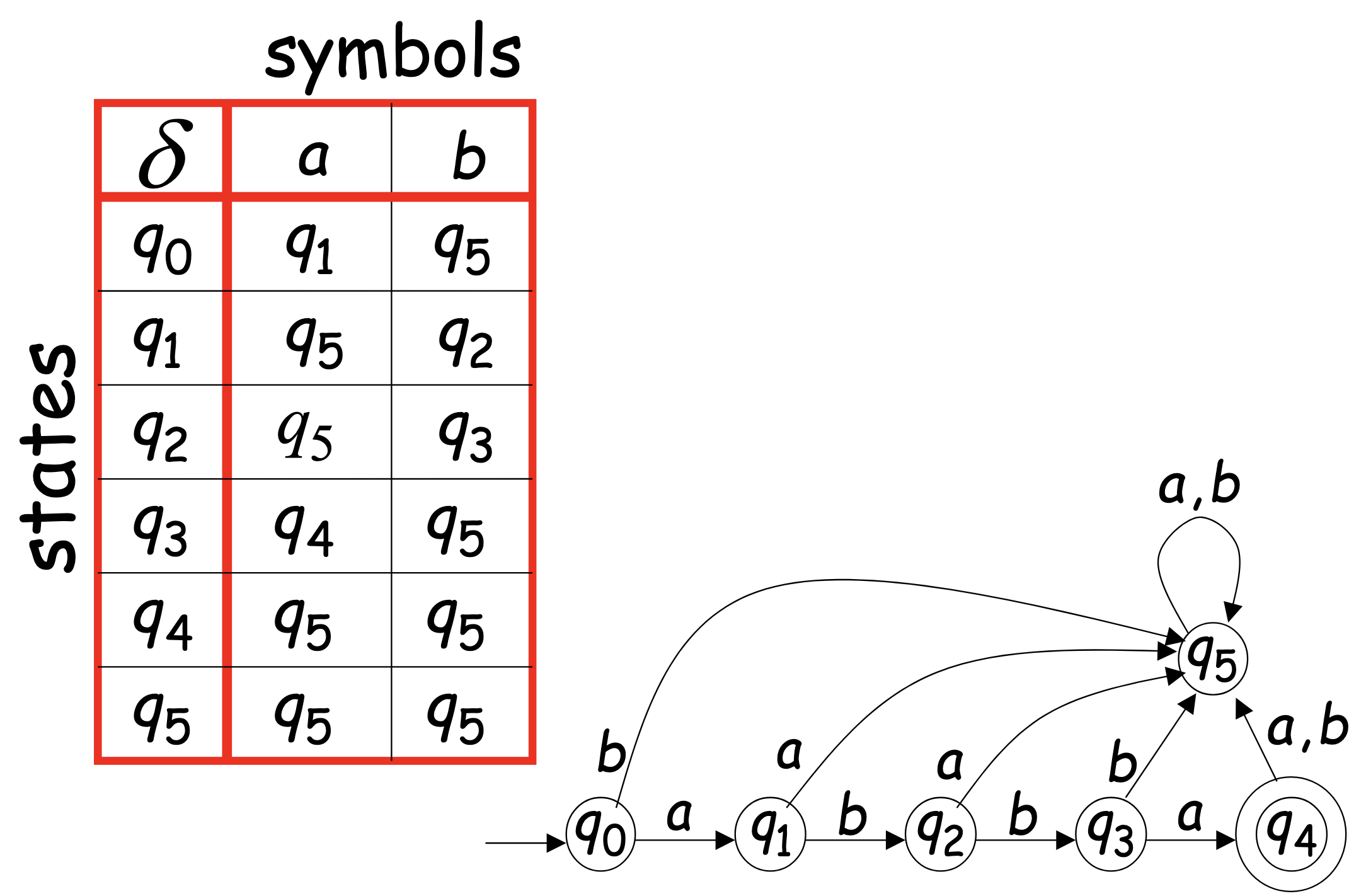
Extended Transition Function

• ${\partial }^{\ast }=Q\ast {\text{Upsigma}}^{\ast }->Q$
• This describes the resulting state after scanning string w from state q In general:
• ${\partial }^{\ast }\left(q,w\right)=q^{\prime }$

Language Accepted by DFA

• Denoted as $L(M)$ and contains all strings accepted by M
• $L\left(M\right)=\left\{w\in {\Sigma }^{\ast }:{\partial }^{\ast }\left(q_0,w\right)\in F\right\}$

DFS vs Pushdown Automata

Pushdown automata which is used for recognizing LL(1) languages are strictly more powerful than DFA’s because PA’s can recognize context-free languages instead of just Regular Languages. Since regular languages are a subset of context free languages, we know that PA’s are more powerful than DFA’s.

The difference is PDA’s have a stack as unbounded memory but both have finite states.