LaPlace Transforms

Definition

The transform is useful for converting differentiation and integration in the time domain into much easier multiplication and division in the Laplace domain. Laplace transforms and their inverses are linear.

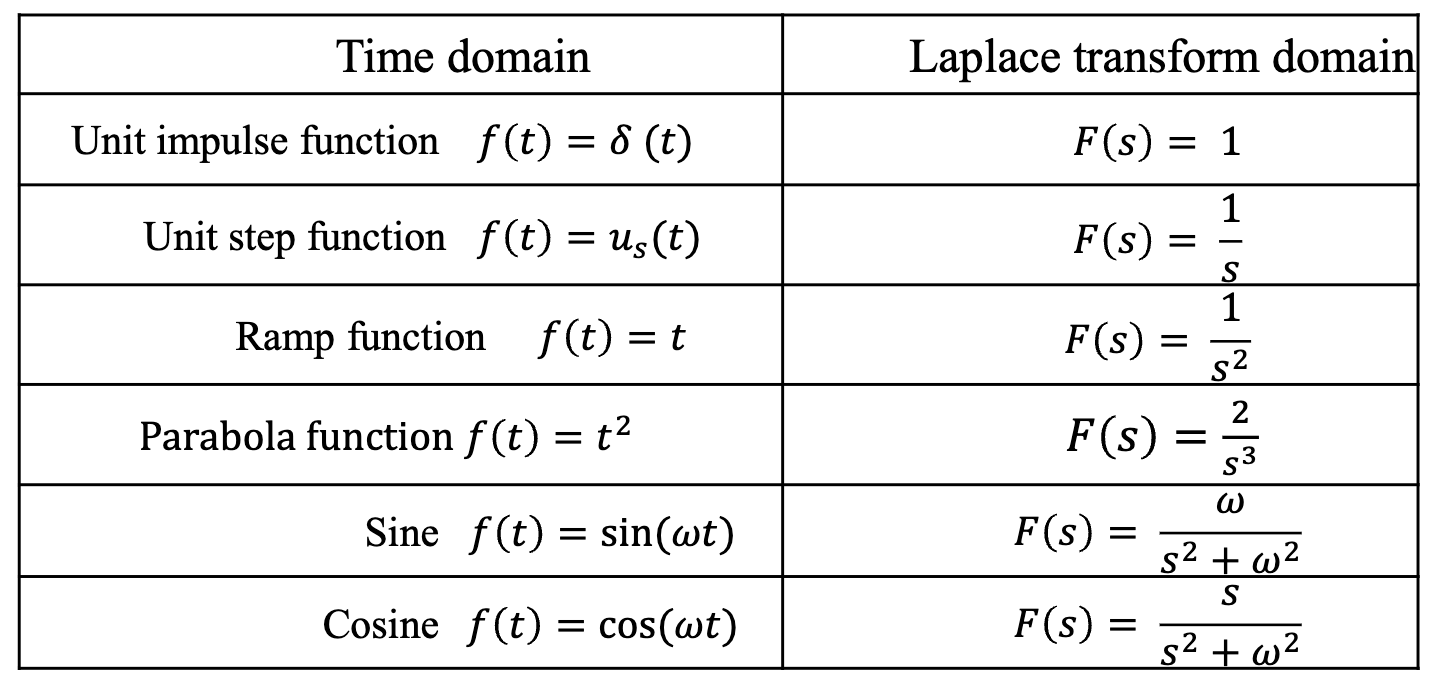
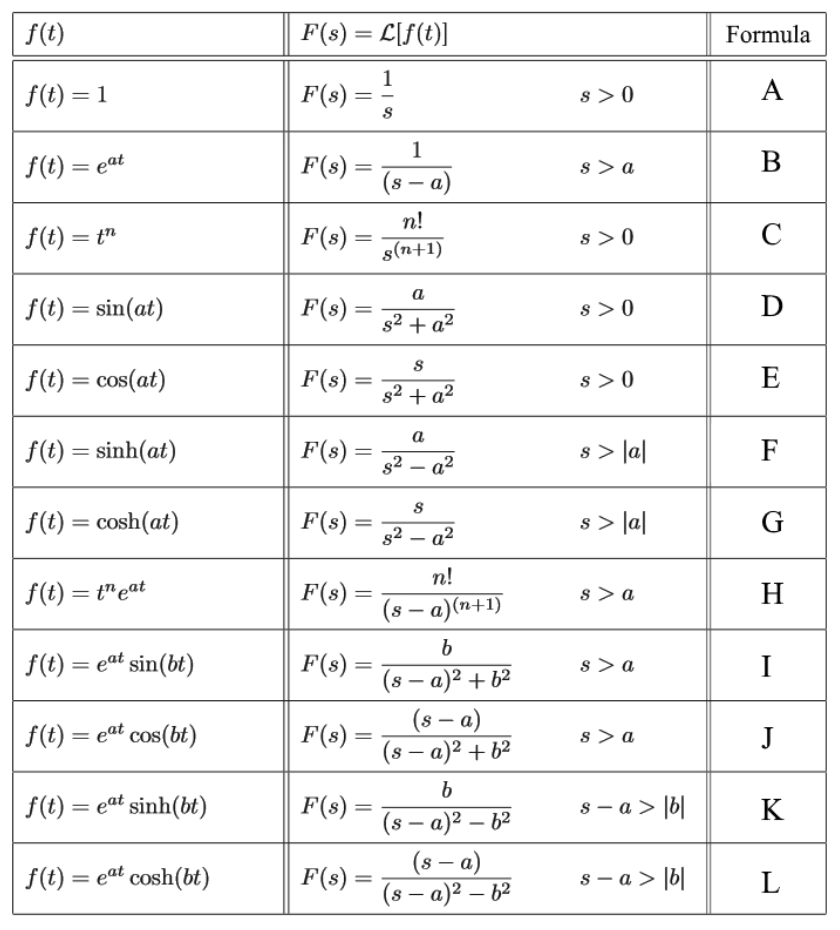
Here are some general transforms (you can look up the rest of these)

The formal definition is $F\left(s\right)=L<f\left(t\right)>:-{\int }_0^{\infty }{e}^{-st}f\left(t\right)dt$

x(t)	x(s)
x’(t)	s
x’’(t)	$s^2$
t	$\frac{1}{s}$
Use a table for this stuff

Properties

• Time delay (shift)
• Linearity
• Differentiation
• Integration
• Time exponential
  • A shift in time exponential weighting in the s domain does the same thing in time
• Convolution

Theorems

• IVT: $y\left(0^{+}\right):-{\lim }_{t\to 0}y\left(t\right)={\lim }_{s\to inf}sY\left(s\right)$
• FVT: $y\left(\infty \right)L={\lim }_{t\to \infty }y\left(t\right)={\lim }_{s\to 0}sY\left(s\right)$ holds only when $y\left(\infty \right)$ exists

We use the LaPlace transforms to create Transfer Functions

You can get the impulse response of a system by doing the inverse LaPlace transform of a transfer function:

• $x\left(t\right)=L^{-1}\left(X\left(s\right)\right)=\frac{1}{2{\pi }_j}{\int }_{-\infty }^{\infty }X\left(j\omega \right)e^{j\omega t}dw$

You can just use the table to do so and probably need to do some Partial Fractional Decomposition to do so