Boundary Value Analysis

We have partitioned input domains into suitable classes using Equivalence Testing, on the assumption that the behaviour of the program is similar.

Some typical programming errors tend to occur near extreme values. This is the point of boundary value testing. This is simpler but complementary to previous techniques.

Sample Conditions

1. First / last / start / finish
2. Min / max / under / over / lowest / highest
3. Empty / full
4. Slowest / fastest / smallest / largest / shortest / longest
5. Next to / farthest from
6. Soonest / latest

Use input variable values at the boundaries (and around their boundaries). The convention here is (min, min+, nom, max-, max). Only change one variable at a time.

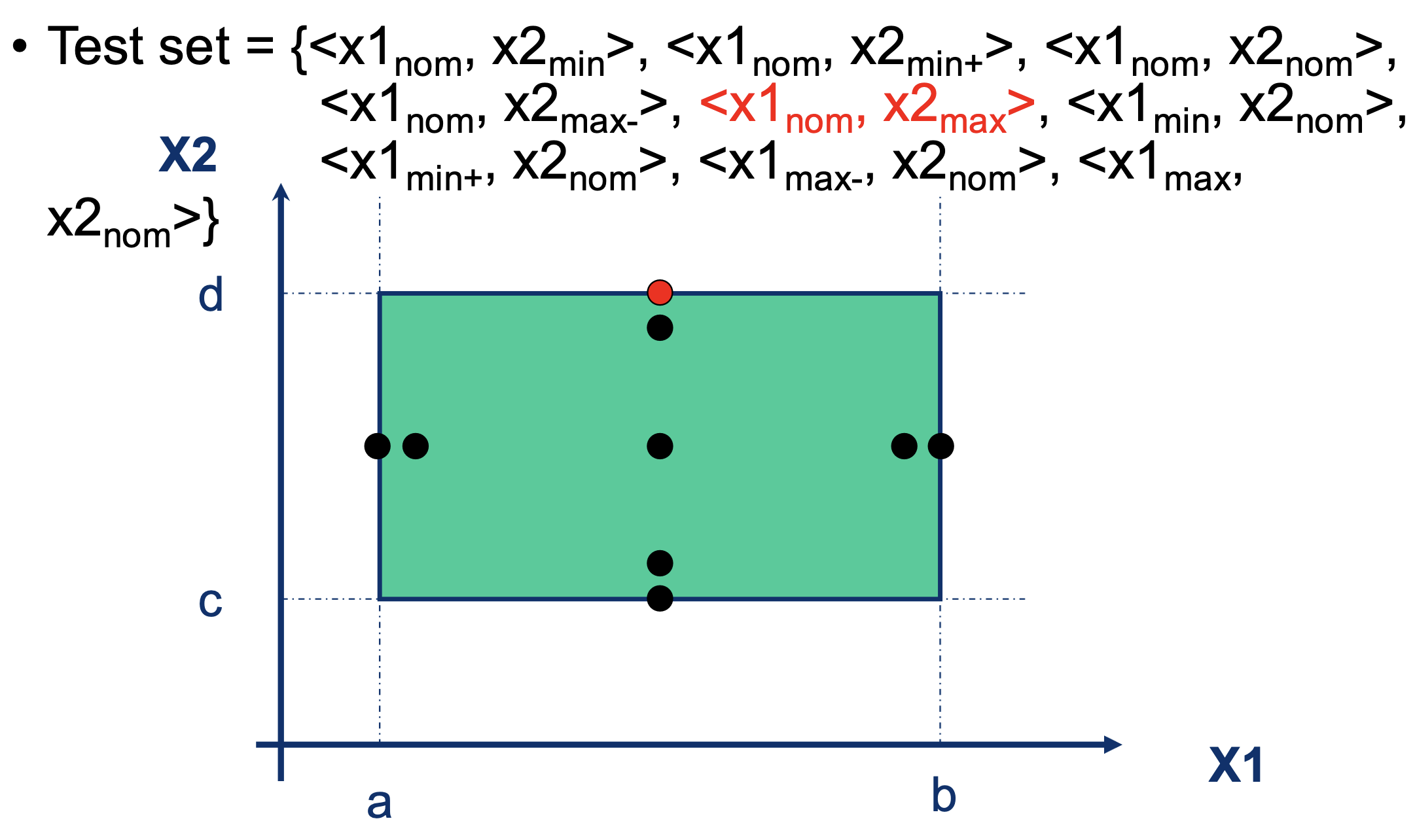
General Case and Limitations

• A function with n variables will generally require $4n+1$ test cases
• Works well with variables that represent bounded physical quantities
• No consideration of the nature of the function and the meaning of variables
• Rudimentary technique that is amenable to robustness testing (requires $6n+1$ test cases)
  • For each boundary condition, include value just beyond the boundary (boundary +- 1) in at least one invalid test case.

Worst Case Testing

Boundary value analysis makes the common assumption that failures originate from one fault related to an extreme value. What happens if more than one value has an extreme value?

Testing a cartesian product of the set $\{min,min+,nom,max-,max\}$ is clearly more thorough than boundary value analysis but is $5^n$ test cases, which is a lot more. This is a good strategy when physical variables have numerous interactions and failure is costly.