Definition
A topological sort is an ordering of the nodes of a directed graph such that if there is a path from node a to node b, then node a appears before node b in the ordering.
Example
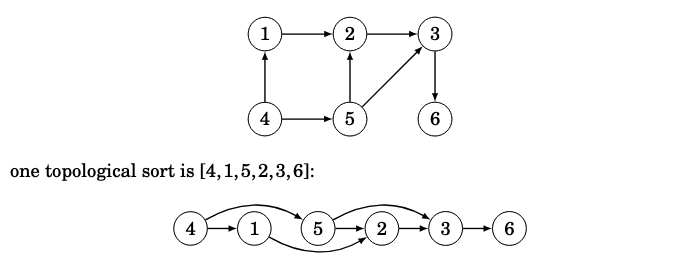
An acyclic graph always has a topological sort, but we cannot topological sort if there is a cycle (no clear beginning and end). DFS can be used to check if there is a cycle, and if there is not, to construct a topological sort.
Algorithm
The idea is to go through the nodes of the graph and always begin a depth-first search at the current node if it has not been processed yet. During the searches, the nodes have three possible states:
- state 0: the node has not been processed
- state 1: the node is under processing
- state 2: the node has been processed
Initially, the state of each node is 0. When a search reaches a node for the first time, its state becomes 1. Finally, after all successors of the node have been processed, its state becomes 2. If the graph contains a cycle, we will find this out during the search, because sooner or later we will arrive at a node whose state is 1. In this case, it is not possible to construct a topological sort.
If the graph does not contain a cycle, we can construct a topological sort by adding each node to a list when the state of the node becomes 2. This list in reverse order is a topological sort.
Implementation:
def dfs(node):
if state[node] == 1:
return False
if state[node] == 2:
return True
state[node] = 1
for neighbour in adjacency[node]:
if not dfs(neighbour):
return False
state[node] = 2
order.append(node)
return True