Geometrical Transformations

Geometrical transformations that are described as a linear equation can be represented as Matrix Mappings.

Rotations

A rotation is an in-plane transformation from ${\mathbb{R}}^2\to {\mathbb{R}}^2$ which rotates $\vec{x}$ counterclockwise through angle $\theta$ to the image $R_{\theta }(\vec{x})$.

This is a linear mapping.

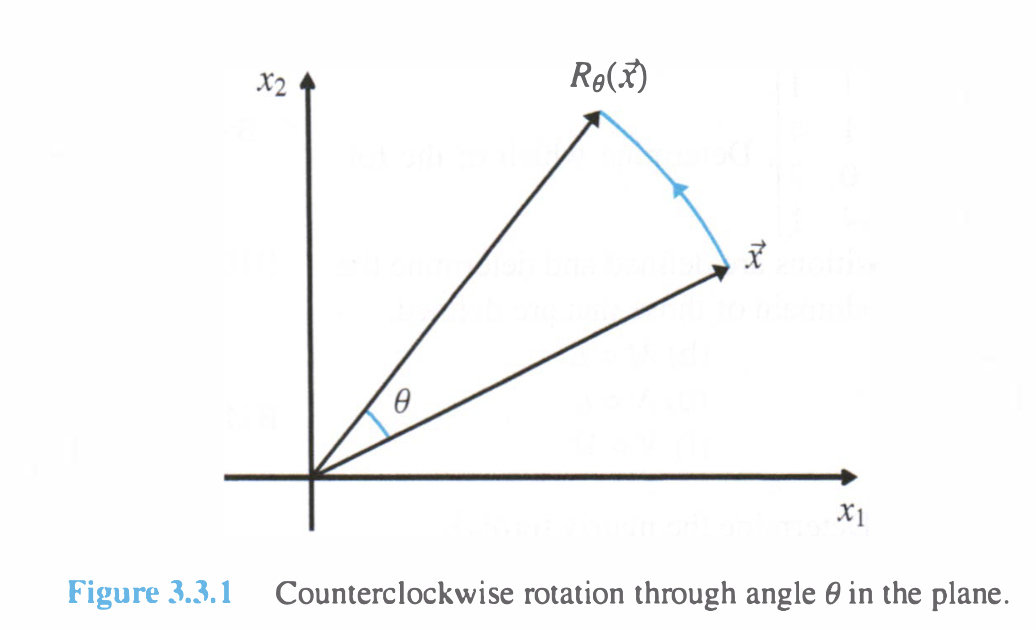
Using the basis of ${\mathbb{R}}^2=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$, we define the rotation matrix as $R_{\theta }=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]$.

In 3D

For a right handed standard basis, this rotation matrix can be extended to $R_{\theta }=\left[\begin{array}{ccc}\cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right]$ which is the transformation about the z axis. This idea can be adapted to rotate about the other axes.

Stretches

This is where all lengths in one particular direction are scaled by $t$ while all lengths in other directions are left unchanged.
This produced the following matrix…
$\left[\begin{array}{cc}t& 0\\ 0& 1\end{array}\right]$

Contractions and Dilations

This is just scaling and has the following matrix $\left[\begin{array}{cc}t& 0\\ 0& t\end{array}\right]$.

Shears

Sometimes a force applied to a rectangle will cause it to deform into a parallelogram. This change can be denoted by $S:{\mathbb{R}}^2\to {\mathbb{R}}^2$ such that $S:(2,0)=(2,0)$ but $S:(0,1)\to (s,1)$. Therefore, $\left[\begin{array}{cc}1& s\\ 0& 1\end{array}\right]$.

Reflections

Let $R:{\mathbb{R}}^{2\to }{\mathbb{R}}^2$ be a reflection across the $x_1$-axis. Then every vector with a point above that axis is mapped by $R$ to a corresponding point in the image vector in the -$x_1$ direction.

This looks like $\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]$.

We can also do this in three dimensions…
Therefore, $\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& -1\end{array}\right]$ performs a reflection about the $x_1{x}_2$ plane (since the negative is in $x_3$).

The general equation for this is $R=I-2\hat{n}{\hat{n}}^T$.