This is about whether or not a variable’s value matters in the future, A variable is live at a program point if there is some path forward where it’s value could be used. It is dead if it will not be used again. The textbook says it looks similar to Three Address Code but I don’t see it?
Exert from Wikipedia
Liveness analysis can determine which sets of variables are live at the same time. Using this information, the compiler can make a graph such that every vertex represents a unique variable in the program. Interference edges connect pairs of vertices which are live at the same time, and preference edges connect pairs of vertices which are involved in move instructions. Register allocation can then be reduced to the problem of K-coloring the resulting graph, where K is the number of registers available on the target architecture. No two vertices sharing an interference edge may be assigned the same colour, and vertices sharing a preference edge should be assigned the same colour if possible. Some of the vertices may be pre-coloured to begin with, representing variables which must be kept in certain registers due to calling conventions or communication between modules. As graph colouring in general is NP-complete, so is register allocation. However, good algorithms exist which balance performance with quality of compiled code.
Analysis
This tells us, for each statement, which variables are currently holding values that might be used in the future. This is the first step in register allocation.
Statements
A statement uses a variable that appears on the RHS of the statement and defines a variable that appears on the LHS.
The dataflow equation templates for liveness analysis are:
Example of analysis:

From this analysis, we can construct an inference graph with a node for each variable where the edges are between nodes that are live at the same time (i.e cannot share a register). We then colour the graph with each colour representing the same register. This is an NP complete problem so you may not get the solution on the first attempt, programatically you actually need to apply Backtracking.
Example Coloured
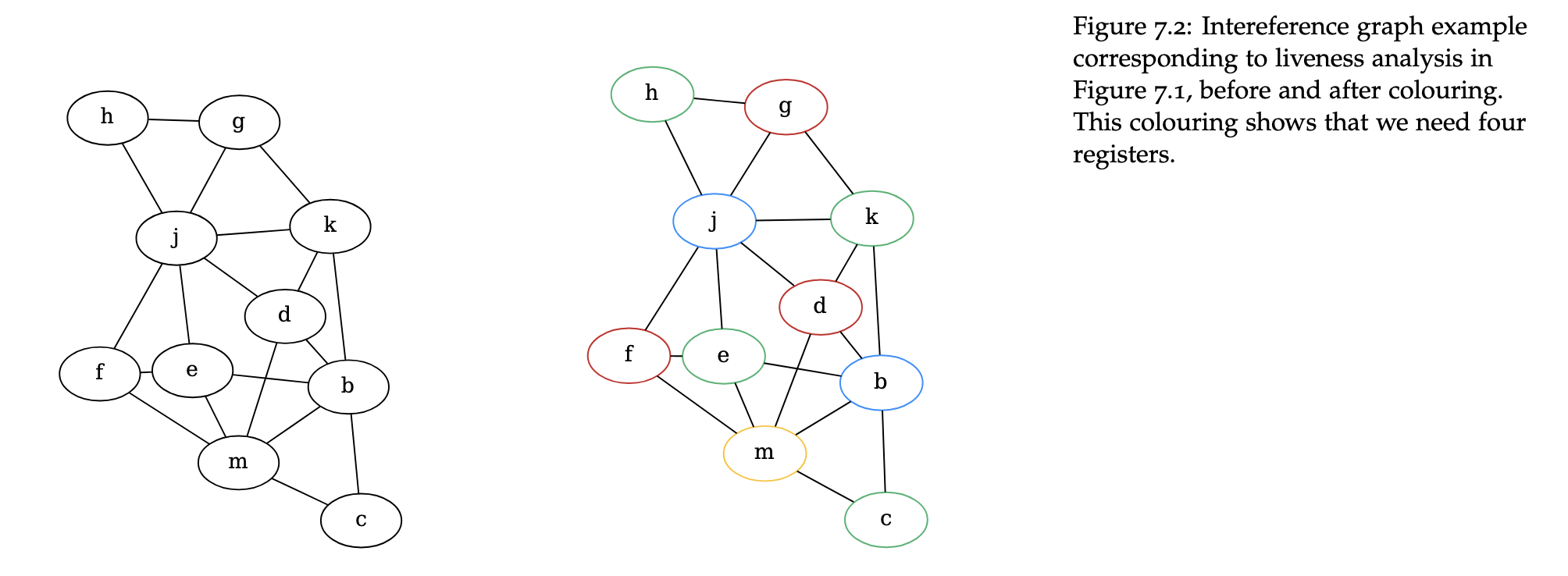
Here in this example, we don’t split j and k into their separate lifetimes, but we could to achieve a more optimal solution.
Example with split lifetimes
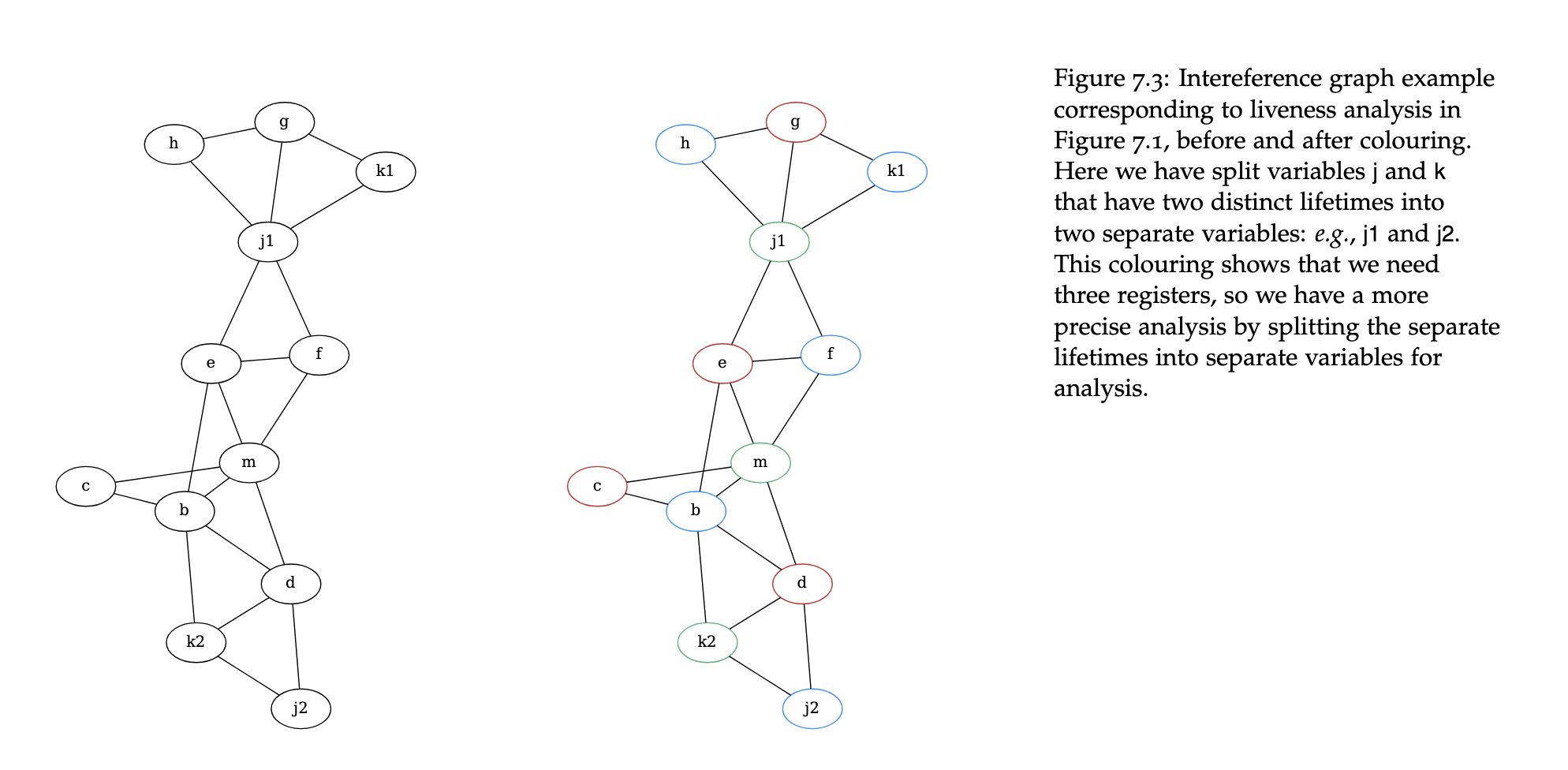
Hint
In general, it seems like the number of registers required is equal to the maximum number of edges for any given node + 1