Triangulation

Triangulation in computer vision is the process of determining a 3D point’s location in space by observing a set of 2D projections (at least 2 images). This is very important for 3D reconstruction and stereo vision.

Requirements

• min(2) images of the same scene
• Calibrated camera extrinsics + intrinsics

Triangulation is projecting rays as pixels and finding where they intersect

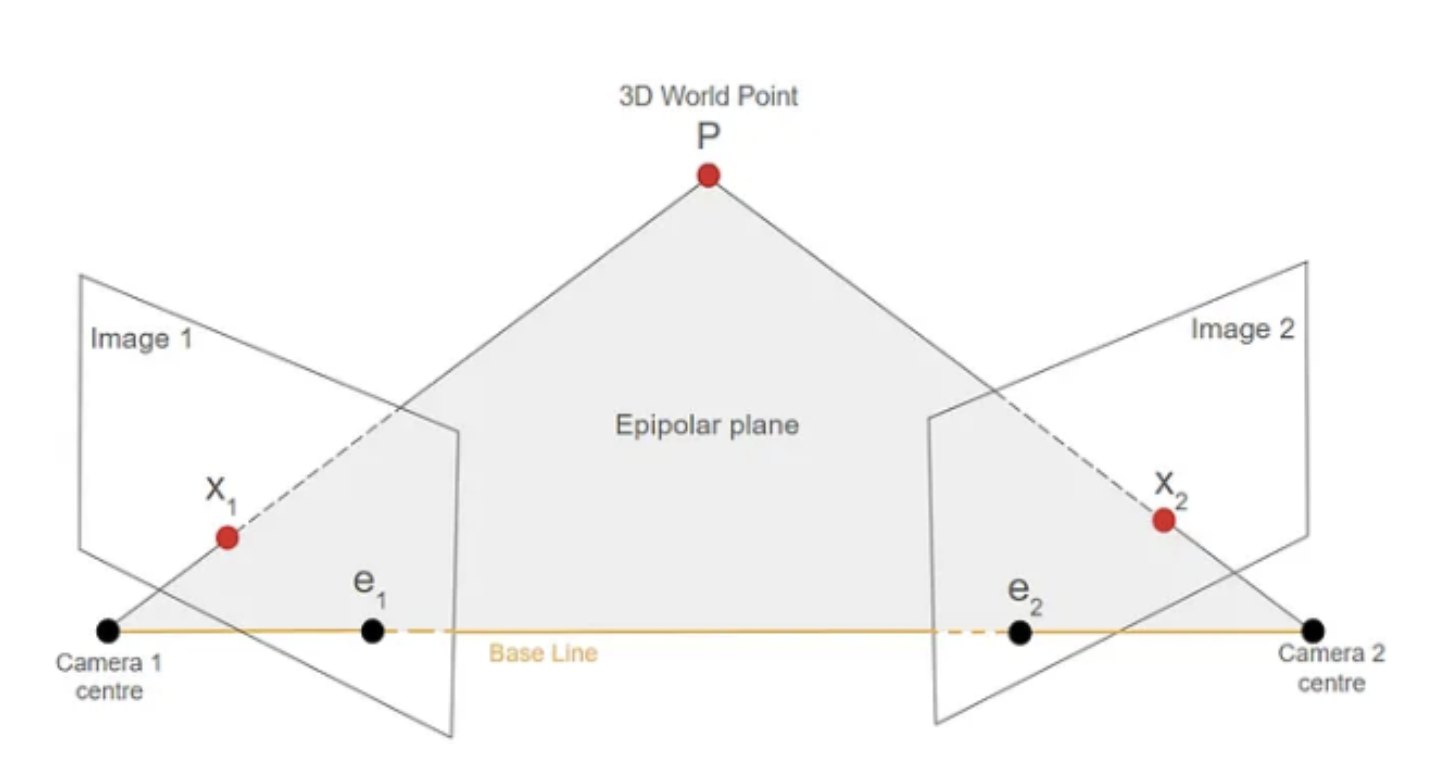
OpenCV uses a pinhole camera model and the DLT Method and the view of a scene is found by projecting a scene’s 3D point into the image plane using a perspective transformation.

The projection matrix is given by $p=A[R|t]P_w$ which is actually the $3D\to 2D$ matrix but the same form is used for $2D\to 3D$. $R$ is the rotation matrix, and $t$ is the translation vector that describes the change of coordinates from the world to the camera frame. The camera intrinsic matrix (also notated as $K$), is the same for 2D → 3D and the other way around as is defined as…

$K=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]$

Where t is defined as $t=-R\ast \text{camera position}$

R can be extracted from MuJoCo if using a simulator as a flat array (where the 9 values of the 3x3 matrix are stored in data_->cam_xmat[0:9]).

Coordinate differences

There are slight differences between MuJoCo’s coordinate frame and OpenCV’s where you need to flip the Y positions and use -Z as forward

$c$ and $f$ are the center of the camera (the pinhole where the rays come from), and the focal lengths respectively.

In the real world, I believe a lot of this information will come from calibration.

#include <vector>
 
struct CameraIntrinsics {
    cv::Mat K;           // 3x3 intrinsic matrix
    cv::Mat dist_coeffs; // distortion coefficients
};
 
struct CameraExtrinsics {
    cv::Mat R;  // 3x3 rotation matrix (world to camera)
    cv::Mat t;  // 3x1 translation vector
};
 
struct CameraPose {
    CameraIntrinsics intrinsics;
    CameraExtrinsics extrinsics;
    cv::Mat P;  // 3x4 projection matrix
};

// MuJoCo cam_xmat columns are the camera's X, Y, Z axes in world coordinates
        // Column 0: camera X axis (right)
        // Column 1: camera Y axis (up)
        // Column 2: camera Z axis (forward, which is -viewing direction in MuJoCo)
 
        // OpenCV camera convention:
        // X: right
        // Y: down
        // Z: forward (into the scene)
 
        // Build rotation matrix for OpenCV convention
        // We need to flip Y (MuJoCo up -> OpenCV down) and use -Z as forward
        cv::Mat R = cv::Mat(3, 3, CV_64F);
 
        // Row 0: camera X axis (right) - same in both
        R.at<double>(0, 0) = cam_mat[0];
        R.at<double>(0, 1) = cam_mat[3];
        R.at<double>(0, 2) = cam_mat[6];
 
        // Row 1: camera Y axis - flip (MuJoCo up -> OpenCV down)
        R.at<double>(1, 0) = -cam_mat[1];
        R.at<double>(1, 1) = -cam_mat[4];
        R.at<double>(1, 2) = -cam_mat[7];
 
        // Row 2: camera Z axis - negate (MuJoCo -Z forward -> OpenCV +Z forward)
        R.at<double>(2, 0) = -cam_mat[2];
        R.at<double>(2, 1) = -cam_mat[5];
        R.at<double>(2, 2) = -cam_mat[8];