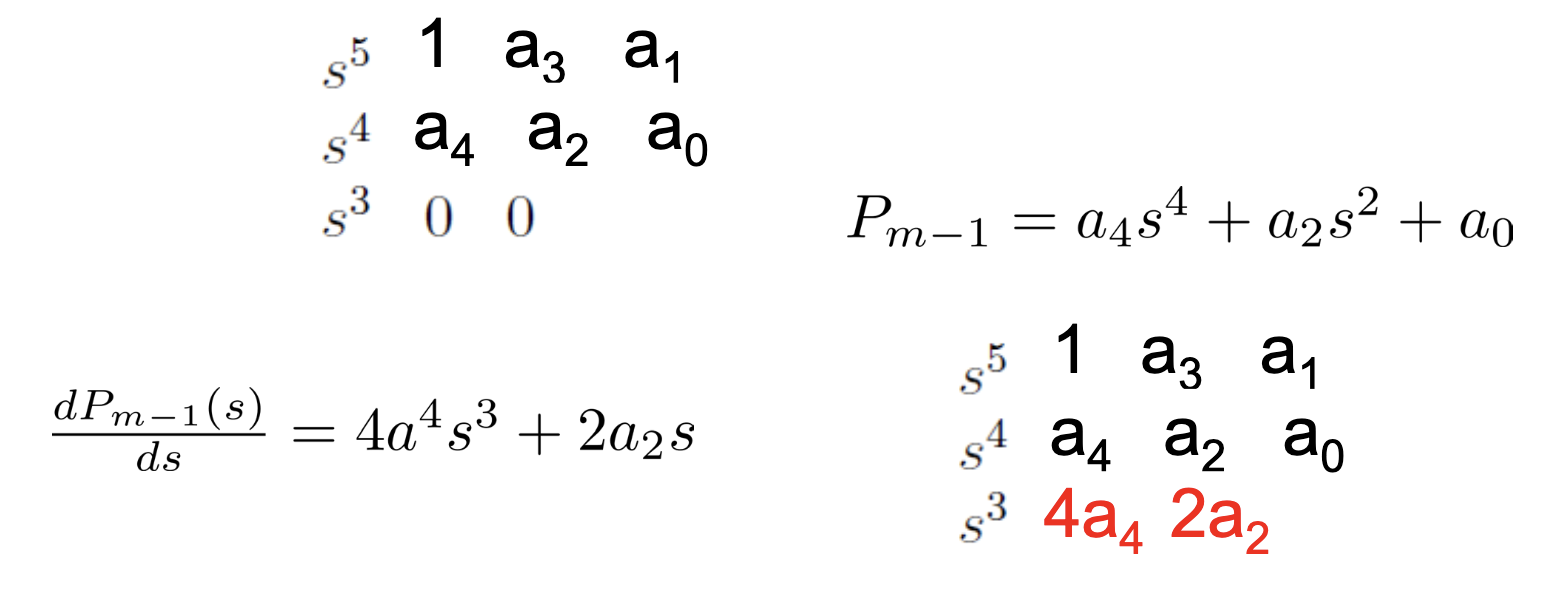Routh Test

This method is based on assembling this table…

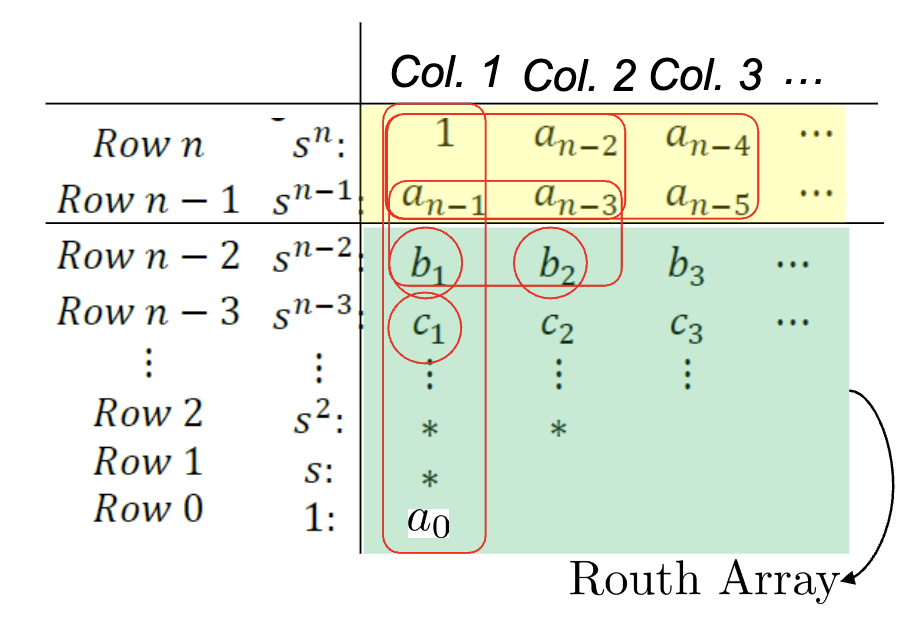
• You fill up the first two rows and then use these equations to fill up the rest…
  • The first row is made of even subtractions of n
  • The second row is made of odd subtractions of n
  • $b_1=-\frac{\det \begin{array}{cc}1& a_{n-2}\\ a_{n-1}& a_{n-3}\end{array}}{a_{n-1}}$
  • $b_2=-\frac{\det \begin{array}{cc}1& a_{n-4}\\ a_{n-1}& a_{n-5}\end{array}}{a_{n-1}}$
  • $c_1=-\frac{\det \begin{array}{cc}{a}_{n-1}& a_{n-3}\\ b_1& b_2\end{array}}{b_1}$
• This will full out triangularly
• The anchor for a row is the leftmost element in the row above where the anchor is the denominator term
• The number of roots with positive real parts is equal to the number of sign changes in the first column
• Empty slots in the right of each row are all zero
• The last element is always $a_0$

Solving

• Simplify transfer function
• Expand denominator
• Write down Rauth table and solve for stability

Special Case 1

• If an element in the first column = 0…
• We replace the zero by a small positive number ($ϵ$)
• Apply the rule by taking the limit $ϵ\to 0$ as needed
• If there is no sign change, the system is not unstable (Happens when some poles lie on the imaginary axis (marginally stable))

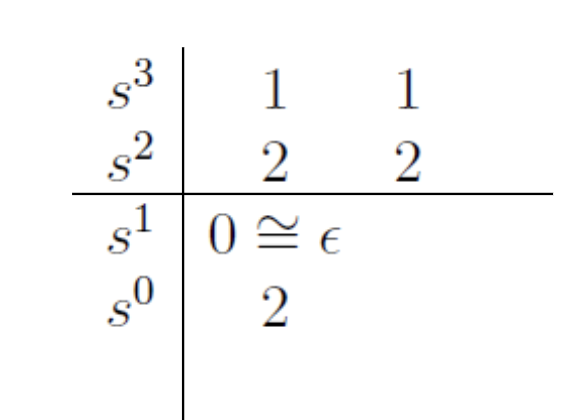
• You basically just skip that cell

Special Case 2

• If all elements in some row are zero
• You can get the row before row m where row m is the row containing all zeroes by using the terms in the row above the row m
• You need to form an auxiliary polynomial $P_{m-1}\left(s\right)$ using these coefficients
• Then, take its derivative
• Use the coefficients of the derivative polynomial to fill up the row containing all zeroes