Finite Automaton Translations

Note

An epsilon ($ϵ$) transition is a transition that the FA can make without consuming an input character.

We can translate NFAs to DFAs. IOW, whatever an NFA can do, a DFA can do.

Regex to DFA

Uses Syntax Directed Translation

• NFAs make it easy to capture disjunctive choice (regex → NFA)
• NFA → DFA
• Minimize and optimize DFA

DFA Minimization

• Merge all accepting states
• Merge all non-accepting states
• Add the error state
• Remove ambiguity (split ambiguous state into 2 states that are distinct)
• Repeat

Some Notation

• The NFA states are labelled with numbers
• The DFA states are labelled with letters
• The DFA have have exponentially more states than the NFA

Granular Examples

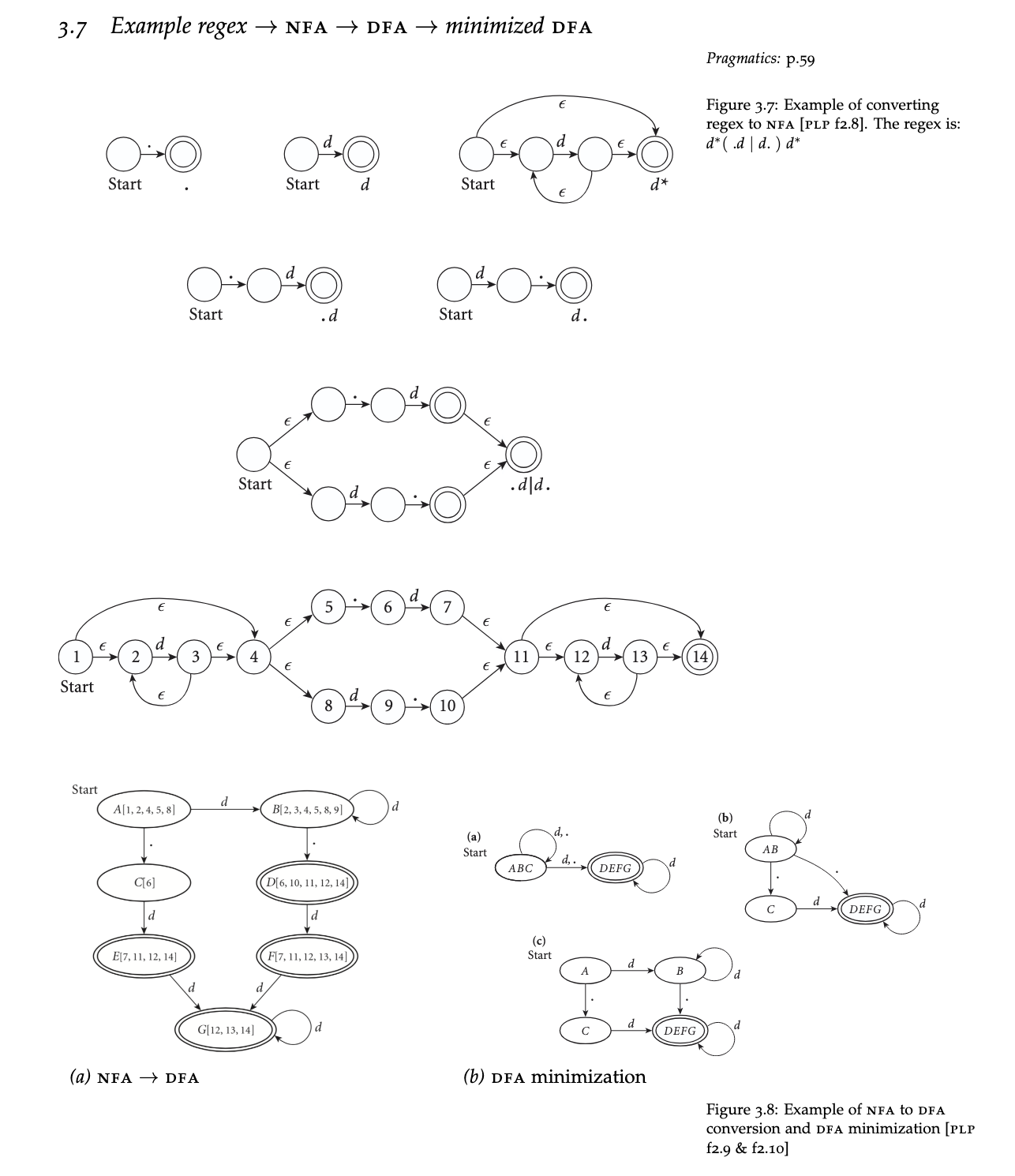
Regex → NFA

Operator transition rules:

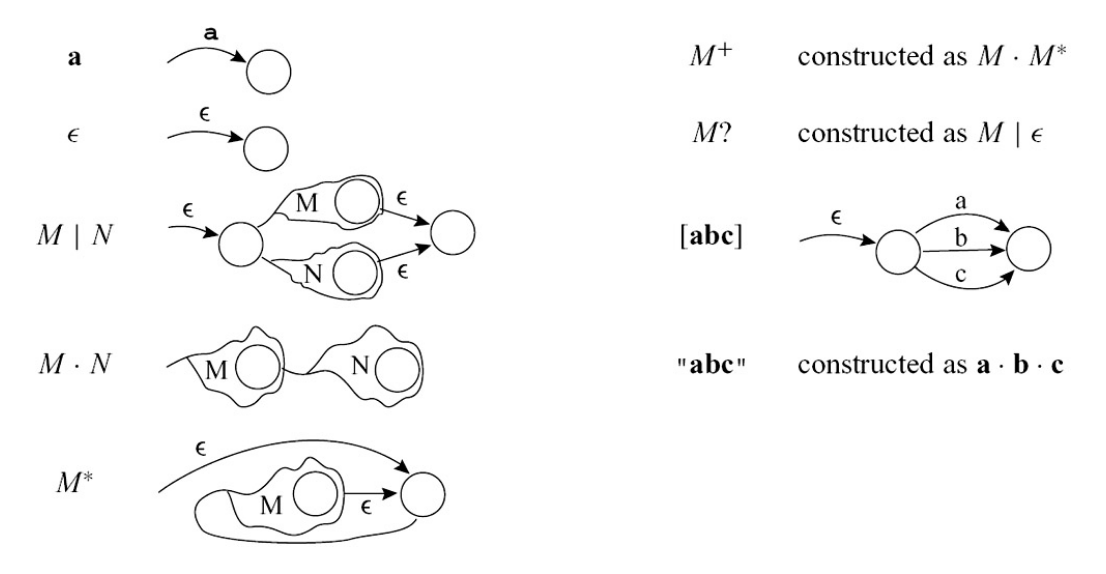
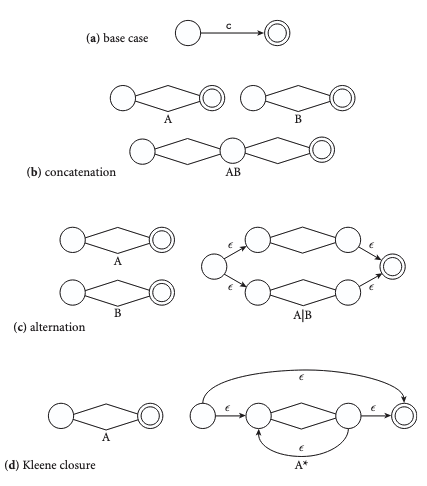
• The strategy…
• Given a regex (ex. $a(abb)\cup b$)
  • Identify the base pieces
    • $a$, $b$, $abb$
    • Create sub-NFAs for these base pieces
  • Connect the sub-NFAs with $ϵ$ transitions using operator rules (where $\cup$, concatenation, kleene star, etc have different $ϵ$ transition rules which are shown above)

NFA → DFA

• Create initial DFA state A which is the NFA start state and all states reachable through $ϵ$
• For each letter $x$, see which DFA states it transitions to from the DFA states included in A and the ones that those states can get to from $ϵ$

DFA Minimization

• Merge all final states into a new final state
• Merge all non-final states into a new non-final state
• This will not be legal at this point because it will have ambiguous transitions
• Iterate through all ambiguous transitions and split the start state such that there are no more ambiguous transitions
• Look for states that do the same thing and condense them into a single state
• Split states with ambiguity into two states
• Repeat until no ambiguity (DFA)

• E2E Example*