Divide and Conquer

The basic idea is:

1. Break the problem into subproblems that are smaller versions of the same problem which can be solved independently
2. Recursively solve these problems
3. Combine the answers

Multiplication

We can multiply 2 n-bit numbers x and y. For now, assume that n is a power of two.

Divide and Conquer Idea: We want to split x and y into their left and right halves where each is $\frac{n}{2}$ bits long. Then, $x=2^{\frac{n}{2}}{x}_l+x_r$ and $y=2^{\frac{n}{2}}{y}_l+y_r$ where each half is $\frac{n}{2}$ bits long and $2^{\frac{n}{2}}$ is a left shift by $\frac{n}{2}$ bits.

Combining these concepts, we can find that $x\ast y=2^n{x}_l{y}_l+2^{n/2}(x_l{y}_r+x_r{y}_l)+x_r{y}_r$. Therefore, to multiply 2 n but numbers, we can instead multiply these four pairs of $\frac{n}{2}$ bit numbers and combine with three additions and two bit shifts as shown in the above equation.

The runtime of this algorithm is $T(n)=4T\left(\frac{n}{2}\right)+O(n)$ where $T(n)$ is the runtime on n-bit numbers. This ends up being $T(n)=O(n^2)$. Instead, if we just compute each term without doing the bit-shifting, our runtimes ends up being $T(n)=3T\left(\frac{n}{2}\right)+O(n)=O(n^{1.59})$.

Formal Algorithm

function multDC(x,y)
Input: 2 n-bit positive integers x and y
Output: x*y

if n = 1:
	return x*y
x_l = leftmost n/2 bits of x (ceil), x_r = rightmost n/2 bits of x (floor)
y_l = leftmost n/2 bits of y (ceil), y_r = rightmost n/2 bits of y (floor)

P1 = multDC(x_l, y_l)
P2 = multDC(x_r, y_r)
P3 = multDC(x_l+x_r, y_l+y_r)
return 2^(2n/2 floor)*P_1+2^(n/2 floor)(P3-P1-P2)+P2

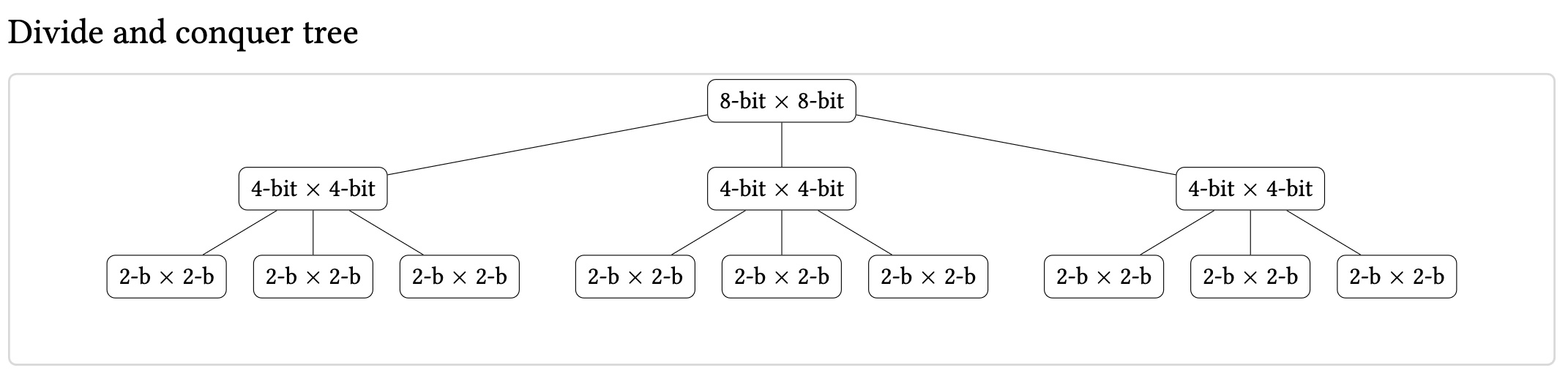
From this tree we can determine the run-time since the divide and conquer tree has a depth of logn and each level k has $3^k$ nodes, the bottom level has $3^{\log n}$ multiplications which after a bunch of log math, ends up being $n^{{\log }_{2}3}$.

Recurrence Relations

We can solve a problem of size n by dividing into a subproblems of size $\frac{n}{b}$ (ceil) and combining their answers in $O(n^d)$ time: $T(n)=aT\left(\lceil \frac{n}{b}\rceil \right)+O(n^d)$.

Masters Theorem

If $T(n)=aT\left(\lceil \frac{n}{b}\rceil \right)+O(n^d)$ for some constant $a>0$, $b>1$, $d\ge 0$. Then:

$\{\begin{array}{llc}O(n^{d)}& & \text{if d >}{\log }_{b}a\\ O(n^{d\log n)}& & \text{if d =}{\log }_{b}a\\ O(n^{{\log }_{b}a})& & \text{if d < }{\log }_{b}a\end{array}$.

See the lecture notes for the proof. But essentially this goes from the bottom levels dominating, to all levels doing the same work, to top levels dominating.

Here, a is the number of subproblems, $\lceil \frac{n}{b}\rceil$ is the size of the sub problem, and d is the factor of work to combine their answers.

See use in Sorting Algorithms, specifically Merge Sort.