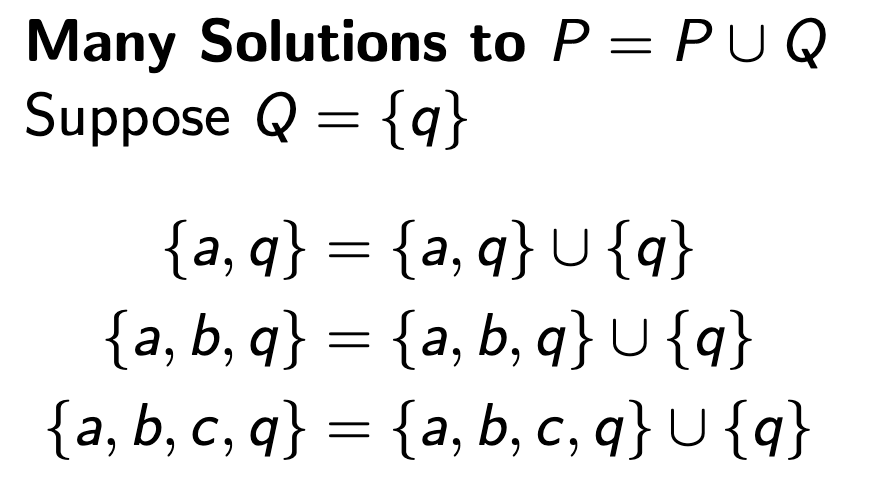Dataflow Analysis

A generic framework to construct and solve a system of equations that describes the set of possible values the program could compute.

A dataflow analysis is defined by a set of equation templates involving these four sets:

• Ins: Expressions available at the beginning
• Outs: Expressions available at the end
• Gen: Set of expressions computed in block
  • All generated expressions specific to what optimization step we are on
  • For generating our available expressions this is everything, for CSE, this is just copies
• Kill: Set of expressions killed by computations in block
  • Looks like this is just uses of generated variables

Dataflow analysis is the general framework which can be applied to things like:

• Available Expressions
• Copy Propagation
• Reaching Definitions

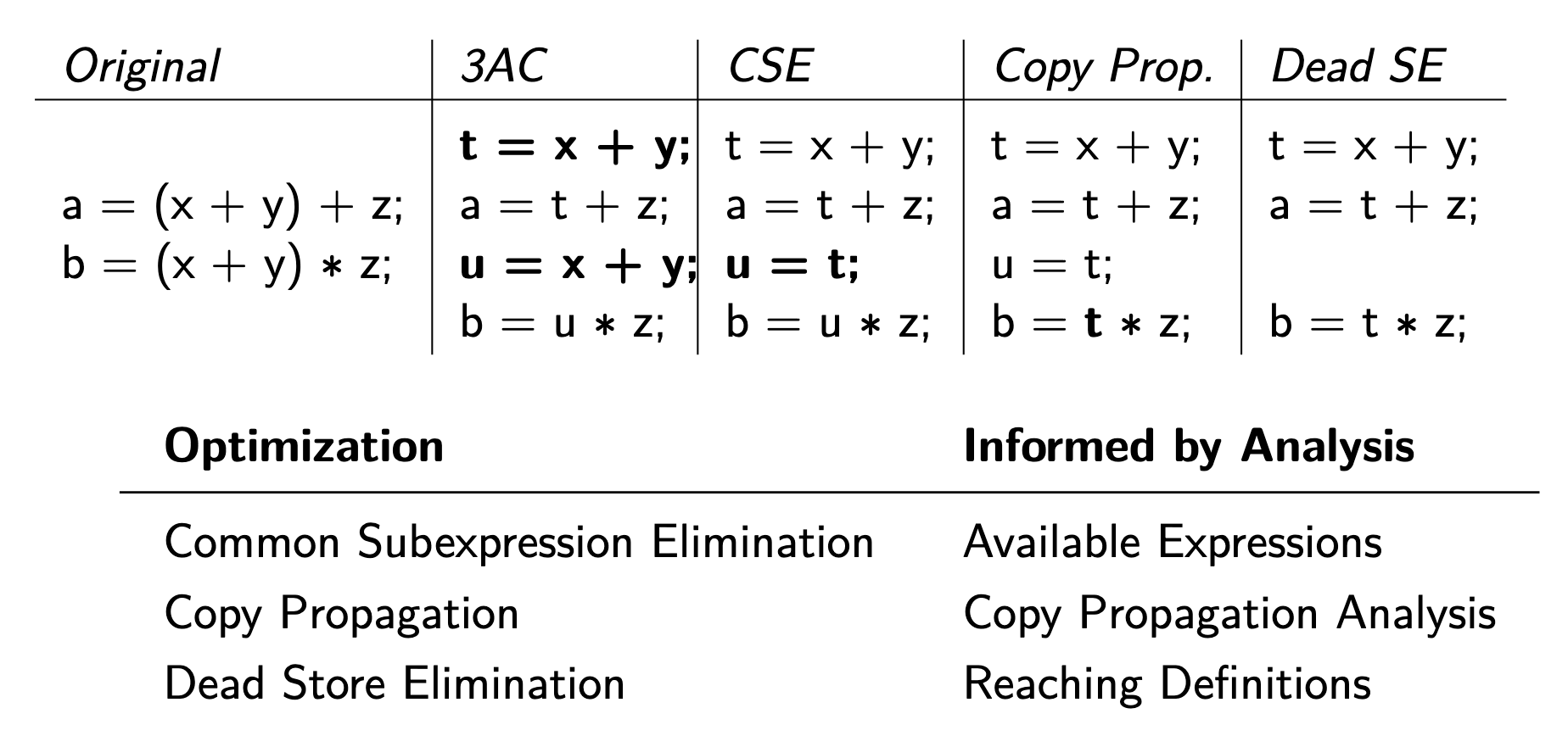
These are the different types of dataflow analyses we can run. These are described in the context of straight line code without branches or loops. These inform different types of Compiler Optimizations.

Summary

Aside Example

a
if (xx) {
	b
	out_b
} else {
	c
	out_c
}
d

For this code block, we want $d=ou{t}_b\bigcap ou{t}_c$ since we only want the available expressions to us.

Our available expressions are…

• $I{n}_s={\bigcap }_{p\in predecessors}Ou{t}_p$
• Except for reaching definitions which is $I{n}_s={\bigcup }_{p\in predecessors}Ou{t}_p$
• $Ou{t}_s=Ge{n}_s\bigcup (I{n}_s-Kil{l}_s)$

These equations are always the same but the definition changes depending on our step of optimization…

Example in copy propagation

Note that in the examples, we see things like $Kil{l}_1=u_3$ meaning that line 1 makes the variable $u$ on line 3 redundant. This is because of our In and Out sets, where line 1 can overwrite line 3 on subsequent calls?, where previous definitions of u are now redundant. We do this instead of $Kil{l}_3=t_1$ because in copy propagation, we only kill copies.

With Loops and Branches

We can symbolically solve most equations but if we have loops or conditions, we could have multiple predecessors.

Solving equations over Sets vs Reals

Loops will give us equations like $P=P\bigcup Q$ because P will be its own predecessor. No problem with reals, for example, $X=X\ast Y$ is fine because want to divide both sides by $X$ and conclude $Y=1$.

There is no division in sets though. There are many solutions to $P=P\bigcup Q$

Here, these are all clearly solutions (fixed points of the equation) to this expression. However we care about the largest or smallest solution.

Iteration to a fixed point if a technique to solve dataflow equations. There are multiple fixed points of a set of equations.

Finding Greatest or Least Fixpoint

1. Each iteration moves up (down) until we get the greatest (least) fixed point
2. We start our iteration based on our confluence operator ($\bigcap :I{n}^0=\{all\}$, $\bigcup :I{n}^0=\{0\}$)
   • Available Expressions uses $\bigcap$
   • Reaching Definitions uses $\bigcup$
3. We move depending on our confluence operator ($\bigcap$ = greatest, $\bigcup$ = least)
4. This process will terminate eventually since our latices are finite

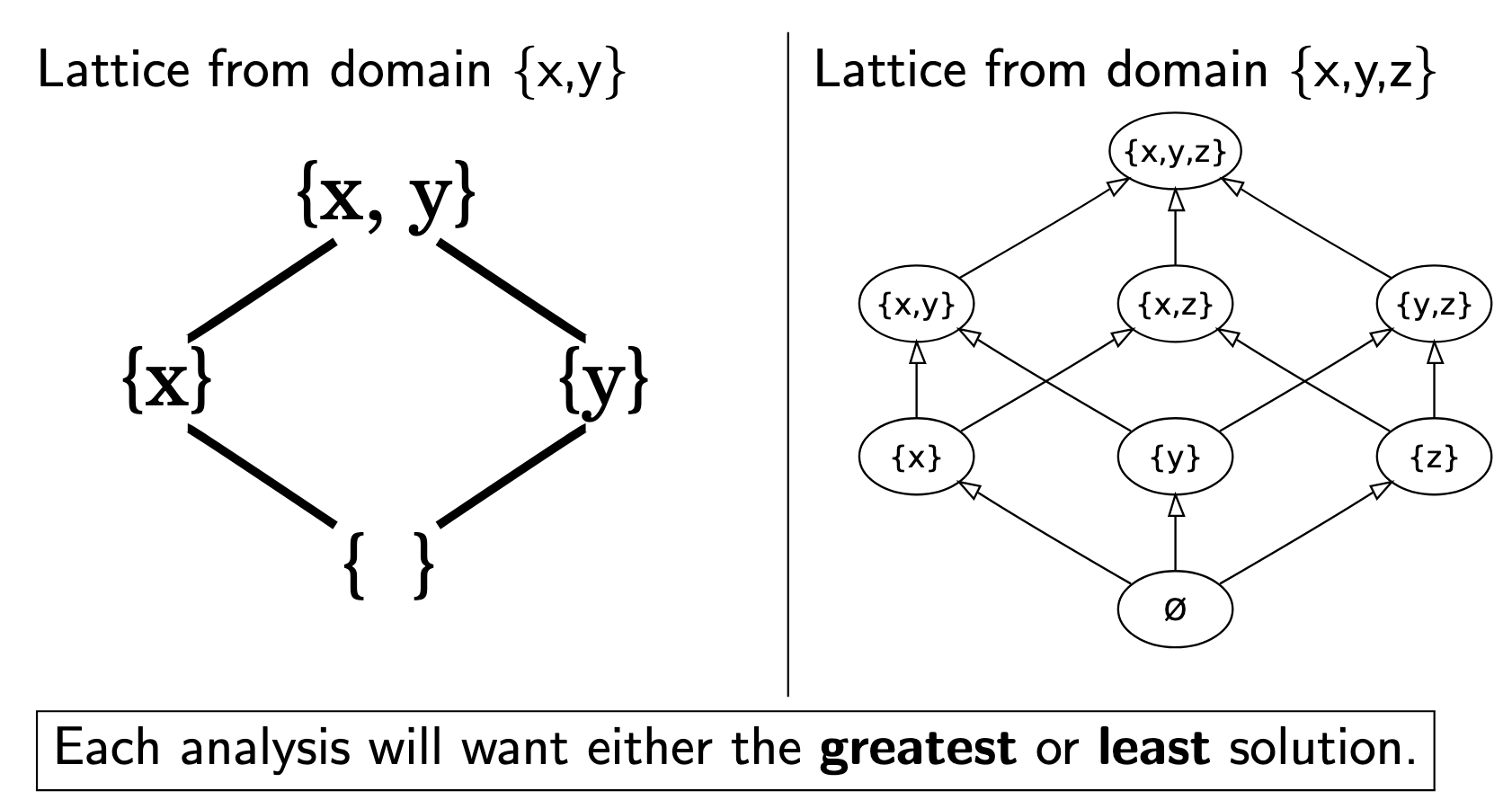
Dataflow sets are drawn from a lattice, each point is a set. If we define $V=\{x,y\}$ and $D=P(V)=2^n$ which is the powerset of V, being all possible subsets of V, we find $D=P(V)=\{0,x,y,xy\}$ which can be visualized in a Hasse diagram.

Info

This is realistically just all combinations of the solution space in a lattice structure if you ever need to draw this.