Argument Principle

Lemma

The argument principle → Let $\Gamma$ be a contour and $G[z]$ be real, rational, and proper.
Then $N=Z-P$

• Where $Z$ and $P$ are the number of zeroes and poles enclosed by $\Gamma$

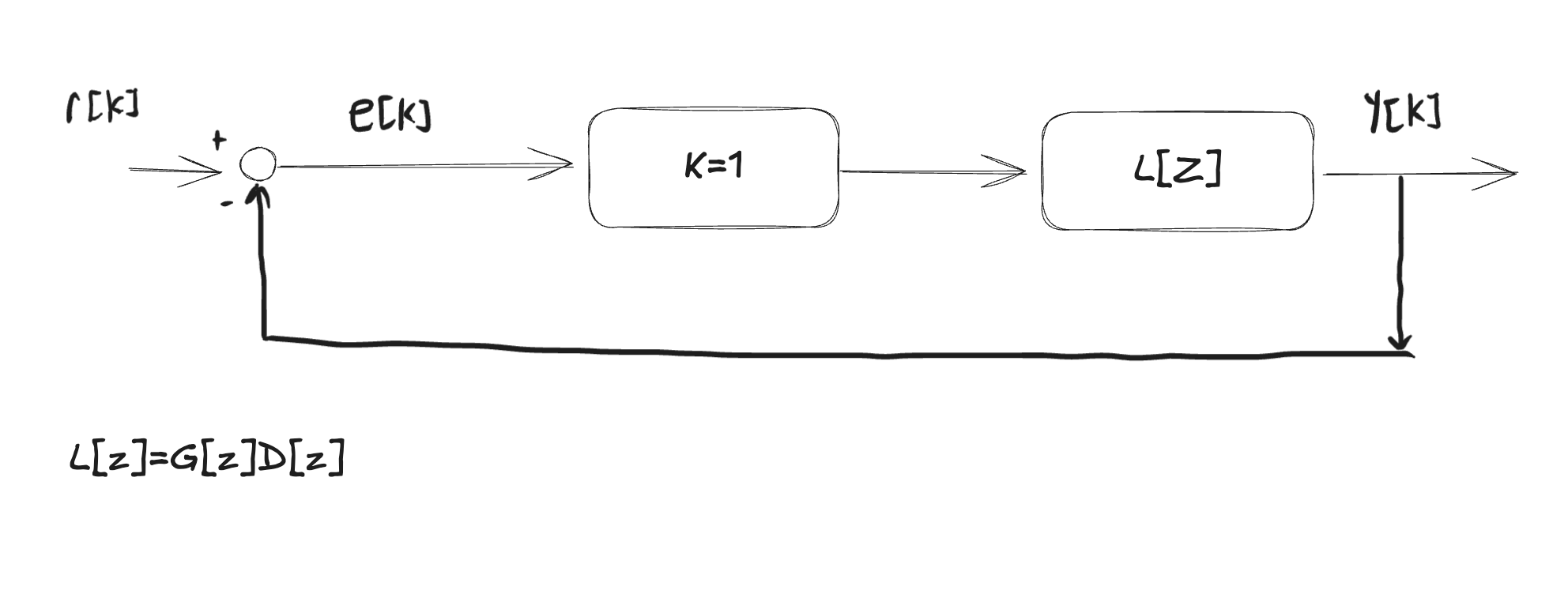
If we choose $\Gamma$ to be the unit circle traversing in the positive direction and choose $V[z]=1+L[z]$

$V[z]=\frac{\Delta [z]}{N[z]G[z]}$ where here, the zeroes of $V[z]$ are the roots of the closed-loop poles and the poles of $V[z]$ are the roots of $N[z]g[z]$ which are the open-loop poles. We already know the open-loop poles in advance.

Applying the argument principle

• $Z=$ # of stable closed-loop poles
• $P$ = # of stable open-loop poles
• Where $N$ is the number of encirclements of:
  • 0 by $V[\Gamma ]=1+L[\Gamma ]$ or by $V[\Gamma ]=1+kL[\Gamma ]$
  • -1 by $L[\Gamma ]$ or by $kL[\Gamma ]$
  • $-\frac{1}{k}$ by $L[\Gamma ]$
• You can make this plot of $L[\Gamma ]$ which is called the Nyquist plot nyquist(L)

Now, the real question here is what happens if we vary $K$ and for which values if any of $k$, is the system closed-loop stable for $k\in \mathbb{R}$