Leetcode - Climbing Stairs

Question

You are climbing a staircase. It takes n steps to reach the top.

Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

Example 1:

Input: n = 2
Output: 2
Explanation: There are two ways to climb to the top.

1. 1 step + 1 step
2. 2 steps

Example 2:
Input: n = 3
Output: 3
Explanation: There are three ways to climb to the top.

1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step

This is a 1ddp problem.

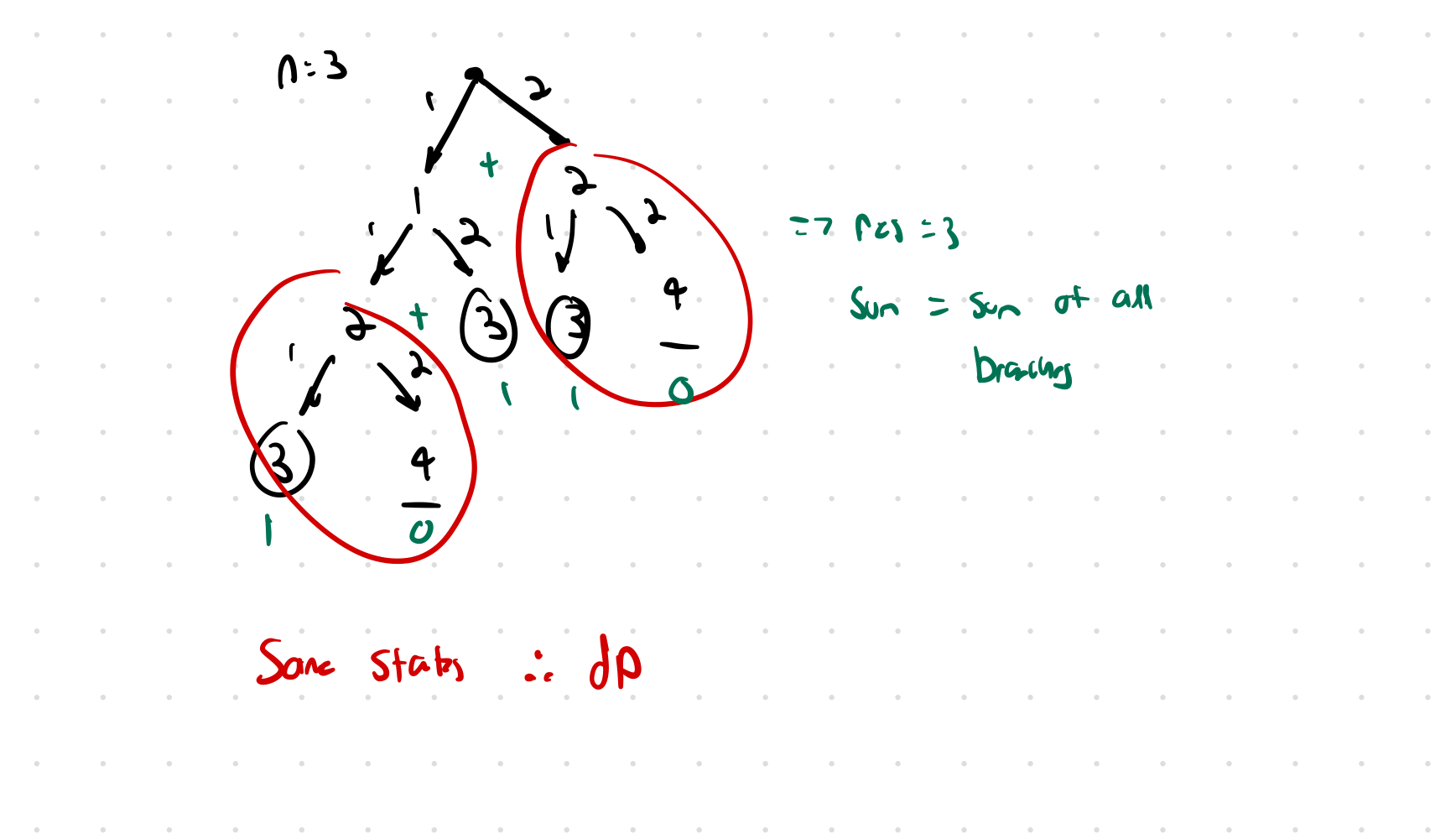
Using Tabulation, we can achieve a runtime of $O(n)$ since we only need to traverse one branch.

Idea

• You can choose 1 or 2 steps which is a binary choice
• We don’t want to go over n
• i == n is the base case
• if a path reaches a base case return 1, otherwise if we overshoot, return 0
• Build an n sized cache to hold the result
• Our result is the sum of all of our branches

Solution